题目内容
已知M是△ABC的边BC上的中点,若
=
,
=
,则
=
| AB |
| a |
| AC |
| b |
| MA |
-
(
+
)
| 1 |
| 2 |
| a |
| b |
-
(
+
)
.| 1 |
| 2 |
| a |
| b |
分析:由平行四边形法则,可得
=
+
.由M为AD的中点,可得
=2
,进而可得答案.
| AD |
| a |
| b |
| AD |
| AM |
解答: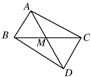 解:如图,以AB、AC为邻边作平行四边形ABDC,
解:如图,以AB、AC为邻边作平行四边形ABDC,
由向量加法的平行四边形法则,
=
+
=
+
.
由M是△ABC的边BC上的中点知,M为AD的中点.
所以
=2
,故
=-
=-
(
+
).
故答案为:-
(
+
)
 解:如图,以AB、AC为邻边作平行四边形ABDC,
解:如图,以AB、AC为邻边作平行四边形ABDC,由向量加法的平行四边形法则,
| AD |
| AB |
| AC |
| a |
| b |
由M是△ABC的边BC上的中点知,M为AD的中点.
所以
| AD |
| AM |
| MA |
| AM |
| 1 |
| 2 |
| a |
| b |
故答案为:-
| 1 |
| 2 |
| a |
| b |
点评:本题考查平面向量基本定理及其意义,涉及向量的加法法则,属中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
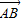 =
=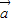 ,
,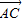 =
=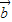 ,则
,则 = .
= .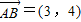 ,则
,则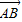 按
按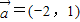 平移后的坐标为(-5,5);
平移后的坐标为(-5,5);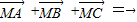 ;
; 的直角三角形面积的最大值为
的直角三角形面积的最大值为 ;
;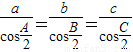 ,则△ABC是等边三角形.
,则△ABC是等边三角形.