题目内容
已知下列命题:①若
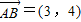 ,则
,则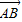 按
按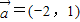 平移后的坐标为(-5,5);
平移后的坐标为(-5,5);②已知M是△ABC的重心,则
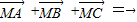 ;
;③周长为
 的直角三角形面积的最大值为
的直角三角形面积的最大值为 ;
;④在△ABC中,若
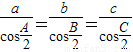 ,则△ABC是等边三角形.
,则△ABC是等边三角形.其中正确的序号是(将所有正确的序号全填在横线上) .
【答案】分析:①据向量的可平移性得到平移后的向量的坐标,
②连接AM并延长交BC与点D,则D为BC的中点,且AM= BC,利用三角形法则用向量
BC,利用三角形法则用向量 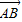 和
和 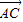 表示即可.
表示即可.
③因为L=a+b+c,c=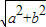 ,两次运用均值不等式即可求解;或者利用三角代换,转化为三角函数求最值问题.
,两次运用均值不等式即可求解;或者利用三角代换,转化为三角函数求最值问题.
④利用正弦定理,求出sin A=sin
A=sin B=sin
B=sin C,推出△ABC是等边三角形.
C,推出△ABC是等边三角形.
解答:解:①∵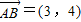
∵向量是可平移的,平移后只改变起点、中的位置,不改变向量的坐标
∴平移后的坐标为(3,4),故错;
②连接AM并延长交BC与点D,则D为BC的中点,且AM= BC,
BC,
由三角形法则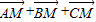 =
=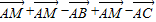 =
=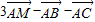 =
=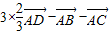
=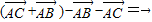
故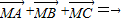 正确;
正确;
③直角三角形的两直角边为a、b,斜边为c,周长L为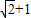 ,面积为s,
,面积为s,
a+b+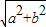 =L≥2
=L≥2 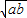 +
+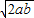 .
.
∴ ≤
≤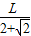 .
.
∴S= ab≤
ab≤ (
( 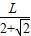 )2
)2
= •[
•[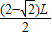 ]2=
]2=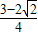 L2=
L2= .故正确;
.故正确;
④∵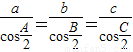 由正弦定理
由正弦定理 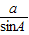 =
= =
=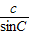 ,得sin
,得sin A=sin
A=sin B=sin
B=sin C,
C,
∴A=B=C⇒a=b=c,则△ABC是等边三角形,正确.
故答案为:②③④.
点评:本题考查向量的性质:向量是可以平移的,平移后与原向量相等;考查向量的三角形法则、平面向量基本定理和向量的表示;考查利用均值不等式解决实际;考查三角函数与正弦定理的应用,考查计算能力逻辑推理能力,常考题型.
②连接AM并延长交BC与点D,则D为BC的中点,且AM=
 BC,利用三角形法则用向量
BC,利用三角形法则用向量 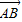 和
和 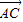 表示即可.
表示即可.③因为L=a+b+c,c=
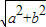 ,两次运用均值不等式即可求解;或者利用三角代换,转化为三角函数求最值问题.
,两次运用均值不等式即可求解;或者利用三角代换,转化为三角函数求最值问题.④利用正弦定理,求出sin
 A=sin
A=sin B=sin
B=sin C,推出△ABC是等边三角形.
C,推出△ABC是等边三角形.解答:解:①∵
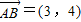
∵向量是可平移的,平移后只改变起点、中的位置,不改变向量的坐标
∴平移后的坐标为(3,4),故错;
②连接AM并延长交BC与点D,则D为BC的中点,且AM=
 BC,
BC,由三角形法则
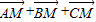 =
=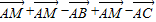 =
=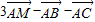 =
=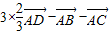
=
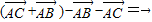
故
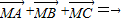 正确;
正确;③直角三角形的两直角边为a、b,斜边为c,周长L为
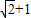 ,面积为s,
,面积为s,a+b+
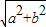 =L≥2
=L≥2 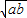 +
+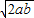 .
.∴
 ≤
≤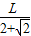 .
.∴S=
 ab≤
ab≤ (
( 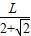 )2
)2=
 •[
•[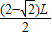 ]2=
]2=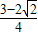 L2=
L2= .故正确;
.故正确;④∵
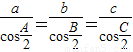 由正弦定理
由正弦定理 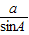 =
= =
=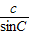 ,得sin
,得sin A=sin
A=sin B=sin
B=sin C,
C,∴A=B=C⇒a=b=c,则△ABC是等边三角形,正确.
故答案为:②③④.
点评:本题考查向量的性质:向量是可以平移的,平移后与原向量相等;考查向量的三角形法则、平面向量基本定理和向量的表示;考查利用均值不等式解决实际;考查三角函数与正弦定理的应用,考查计算能力逻辑推理能力,常考题型.

练习册系列答案
相关题目