题目内容
已知函数f(x)=log2x,等比数列{an}的首项a1>0,公比q=2,若f(a2a4a6a8a10)=25,则f(a1)+f(a2)+…+f(a2009)=
- A.1004×2008
- B.1004×2009
- C.1005×2008
- D.1005×2009
B
分析:先根据f(a2a4a6a8a10)=25以及等比数列{an}的首项a1>0,公比q=2,可求出a1,从而求出f(an),再利用等差数列求和公式解之即可求出所求.
解答:由若f(a2a4a6a8a10)=25,得: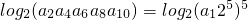 =5log2a1+25=25
=5log2a1+25=25
所以5log2a1=0,所以a1=1,
则f(a1)+f(a2)+…+f(a2009)=log2a1+log2a2+…+log2a2009
=log2(a1a2…a2009)=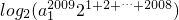 =
=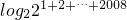 =1004×2009.
=1004×2009.
故选B.
点评:本题主要考查了数列与函数的综合,同时考查了等差数列求和,属于中档题.
分析:先根据f(a2a4a6a8a10)=25以及等比数列{an}的首项a1>0,公比q=2,可求出a1,从而求出f(an),再利用等差数列求和公式解之即可求出所求.
解答:由若f(a2a4a6a8a10)=25,得:
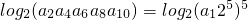 =5log2a1+25=25
=5log2a1+25=25所以5log2a1=0,所以a1=1,
则f(a1)+f(a2)+…+f(a2009)=log2a1+log2a2+…+log2a2009
=log2(a1a2…a2009)=
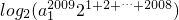 =
=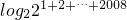 =1004×2009.
=1004×2009.故选B.
点评:本题主要考查了数列与函数的综合,同时考查了等差数列求和,属于中档题.

练习册系列答案
相关题目