题目内容
已知函数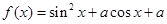 ,
, .
.
(1)当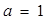 时,求函数
时,求函数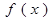 的最大值;
的最大值;
(2)如果对于区间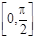 上的任 意一个
上的任 意一个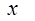 ,都有
,都有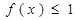 成立,求
成立,求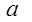 的取值范围.
的取值范围.
(1)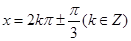 时,
时, ;(2)
;(2)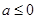 .
.
解析试题分析:(1)当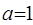 时,
时,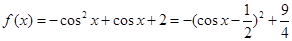
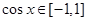 ,所以当
,所以当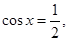 即
即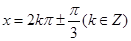 时,
时, …5分
…5分
(2)依题得 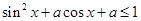 即
即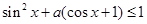 对任意
对任意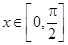 恒成立
恒成立
而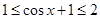 所以
所以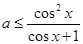 对任意
对任意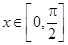 恒成立 7分
恒成立 7分
令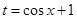 ,则
,则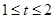 ,所以
,所以 对任意
对任意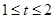 恒成立,于是
恒成立,于是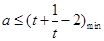 9分
9分
又因为 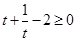 ,当且仅当
,当且仅当 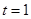 ,即
,即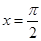 时取等号
时取等号
所以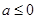 12分
12分
(其他方法,酌情给分)
考点:三角函数同角公式,二次函数的图象和性质,不等式恒成立问题。
点评:中档题,本题利用三角函数同角公式,转化成二次函数闭区间的最值问题。不等式恒成立问题,往往利用“分离参数法”,转化成求函数的最值问题,本题对高一学生来说,是一道较难的题目。

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
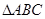 中,角
中,角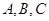 所对的边分别为
所对的边分别为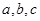 ,且
,且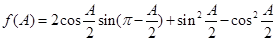 .
.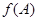 的最大值;
的最大值;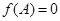 ,
,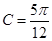 ,
,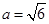 ,求
,求 的值.
的值.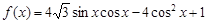 .
.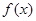 在
在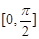 上的值域;
上的值域;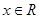 ,不等式
,不等式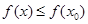 恒成立,求
恒成立,求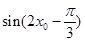 .
. ,
, ,且
,且 的最小正周期为
的最小正周期为
 的值;
的值; ,解方程
,解方程 ;
; 中,
中, ,
, ,且
,且 为锐角,求实数
为锐角,求实数 的取值范围.
的取值范围.  ,
, .
. 的最大值和最小值;
的最大值和最小值; 在
在 的取值范围.
的取值范围.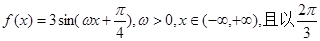 为最小正周期.
为最小正周期.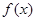 的解析式;
的解析式;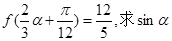 的值.
的值. 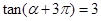 ,求
,求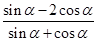 的值;
的值;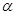 为第二象限角,化简
为第二象限角,化简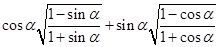
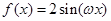 ,其中常数
,其中常数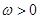 ;
; 在
在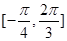 上单调递增,求
上单调递增,求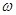 的取值范围;
的取值范围;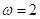 ,将函数
,将函数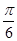 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数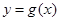 的图像,区间
的图像,区间 (
(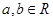 且
且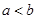 )满足:
)满足: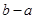 的最小值.
的最小值.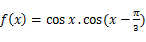
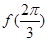 的值;
的值;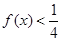 成立的x的取值集合
成立的x的取值集合