题目内容
数列{ }满足a1=1,a2=1,
}满足a1=1,a2=1, =
= +
+ (n∈N﹡,n≥3).从该数列的前15项中随机抽取一项,则它是3的倍数的概率为
(n∈N﹡,n≥3).从该数列的前15项中随机抽取一项,则它是3的倍数的概率为
A. | B. | C. | D. |
B
解析试题分析:根据题意,由于数列{ }满足a1=1,a2=1,
}满足a1=1,a2=1, =
= +
+ (n∈N﹡,n≥3),则
(n∈N﹡,n≥3),则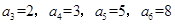 依次类推,则可知该数列的前15项为1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,那么可知在这里是3的倍数的数有3个,3,21,144,则由古典概型概率可知,所求的概率为3:15=1:5=0.2,故答案为B.
依次类推,则可知该数列的前15项为1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,那么可知在这里是3的倍数的数有3个,3,21,144,则由古典概型概率可知,所求的概率为3:15=1:5=0.2,故答案为B.
考点:古典概型概率
点评:主要是考查了古典概型的概率的计算,属于基础题。

练习册系列答案
相关题目
某人射击5枪,命中3枪,3枪中恰有2枪连中的概率为( )
A. | B. | C. | D. |
在平面区域 内任意取一点
内任意取一点 内的概率是( )
内的概率是( )
A. | B. | C. | D. |
从只含有二件次品的10个产品中取出三件,设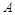 为“三件产品全不是次品”,
为“三件产品全不是次品”,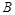 为“三件产品全是次品”,
为“三件产品全是次品”,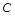 为“三件产品不全是次品”,则下列结论正确的是:
为“三件产品不全是次品”,则下列结论正确的是:
A.事件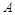 与 与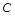 互斥 互斥 | B.事件C是随机事件 |
| C.任两个均互斥 | D.事件B是不可能事件 |
一个口袋中装有2个白球和3个黑球,则先摸出一个白球后放回,再摸出一个白球的概率是( )
A.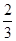 | B.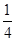 | C.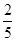 | D.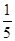 |
 ,若从区间
,若从区间 内随机选取一个实数
内随机选取一个实数 ,则所选取的实数
,则所选取的实数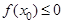 的概率为 ( )
的概率为 ( )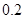



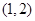 内随机取个实数
内随机取个实数 ,则直线
,则直线 ,直线
,直线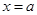 与
与 轴围成的面积大于
轴围成的面积大于 的概率是( )
的概率是( )



 的二项展开式中任取
的二项展开式中任取 项,
项, 表示取出的
表示取出的 项系数为奇数的概率. 若用随机变量
项系数为奇数的概率. 若用随机变量 表示取出的
表示取出的 ( )
( )



 满足约束条件
满足约束条件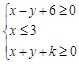 ,且
,且 的最小值为6.若实数
的最小值为6.若实数 则点
则点 落在上述区域内的概率为( )
落在上述区域内的概率为( )


