题目内容
在
的二项展开式中任取
项，
表示取出的项中有
项系数为奇数的概率. 若用随机变量
表示取出的项中系数为奇数的项数，则随机变量的数学期望
（ ）
A． | B． | C． | D． |
D
解析试题分析：根据题意，由于在的二项展开式中任取项，表示取出的项中有项系数为奇数的概率. 因为各项的系数为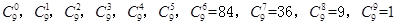
，用随机变量表示取出的项中系数为奇数的项数，则随机变量的数学期望，故答案为D.
考点：随机变量分布列
点评：主要是考查了二项式定理以及随机变量分布列的运用，属于基础题。
练习册系列答案
相关题目
在区间[0，
]上随机取一个数x，则事件“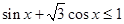
”发生的概率为（ ）
A． | B． | C． | D． |
下列现象是随机事件的是( )
| A．天上无云下大雨 |
| B．同性电荷，相互排斥 |
| C．没有水分，种子发芽 |
| D．从分别标有1,2,3,4,5,6,7,8,9,10的10张号签中任取一张，得到1号签 |
设函数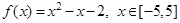
，若从区间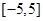
内随机选取一个实数
,则所选取的实数满足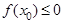
的概率为（ ）
| A．0.5 | B．0.4 | C．0.3 | D．0.2 |
一个工人看管三台机床，在一小时内，这三台机床需要工人照管的概率分别0.9、0.8、0.7，则没有一台机床需要工作照管的概率为 （ ）
| A．0.006 | B．0.018 | C．0.06 | D．0.014 |
}满足a1＝1，a2＝1，
＋
（n∈N﹡，n≥3）．从该数列的前15项中随机抽取一项，则它是3的倍数的概率为
在集合﹛1，2，3，4…，10﹜中任取一个元素，所取元素恰好满足方程
cos （30°·x ）=" 1/2" 的概率为（ ）
| A．1/3 | B．1/4 | C．1/5 | D．1/6 |
从一个不透明的口袋中摸出红球的概率为1/5,已知袋中红球有3个,则袋中共有除颜色外完全相同的球的个数为( ).
| A．5个 | B．15个 | C．10个 | D．8个 |
