题目内容
一个口袋中装有2个白球和3个黑球,则先摸出一个白球后放回,再摸出一个白球的概率是( )
A.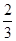 | B.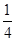 | C.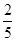 | D.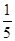 |
C
解析试题分析:因为题目中是有放回的抽取,因此不是条件概率而是等可能性事件概率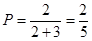
考点:等可能性事件概率
点评:此类型概率的求解首先需要找到所有的基本事件种数与满足题意要求的基本事件种数,求其比值即可

练习册系列答案
 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
从一个不透明的口袋中摸出红球的概率为1/5,已知袋中红球有3个,则袋中共有除颜色外完全相同的球的个数为( ).
| A.5个 | B.15个 | C.10个 | D.8个 |
某学生解选择题出错的概率为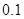 ,该生解三道选择题至少有一道出错的概率是( )
,该生解三道选择题至少有一道出错的概率是( )
A.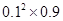 | B.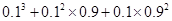 |
C.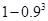 | D.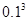 |
掷两颗骰子,所得点数之和为 ,那么
,那么 =4表示的随机试验结果是( )
=4表示的随机试验结果是( )
| A.一颗是3点,一颗是1点 | B.两颗都是2点 |
| C.两颗都是4点 | D.一颗是3点,一颗是1点或两颗都是2点 |
已知某一随机变量ξ的概率分布列如下,且E(ξ)=6.3,则a的值为( )
| ξ | 4 | a | 9 |
| P | 0.5 | 0.1 | b |
在某一试验中事件A出现的概率为 ,则在
,则在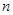 次试验中
次试验中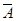 出现
出现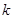 次的概率为( )
次的概率为( )
A.1-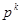 | B.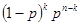 | C.1-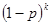 | D.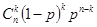 |
 }满足a1=1,a2=1,
}满足a1=1,a2=1, +
+ (n∈N﹡,n≥3).从该数列的前15项中随机抽取一项,则它是3的倍数的概率为
(n∈N﹡,n≥3).从该数列的前15项中随机抽取一项,则它是3的倍数的概率为



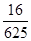
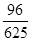
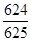
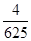
 与
与 相互独立,且
相互独立,且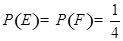 ,则
,则 ( )
( ) .
.  ;
;  .
.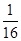 ;
;  .
.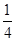 ;
;  .
.