题目内容
已知函数y=2sin ,
,
(1)求它的振幅、周期、初相;
(2)用“五点法”作出它在一个周期内的图象;
(3)说明y=2sin 的图象可由y=sinx的图象经过怎样的变换而得到.
的图象可由y=sinx的图象经过怎样的变换而得到.
 ,
,(1)求它的振幅、周期、初相;
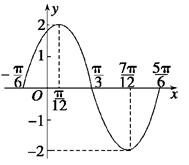
(2)用“五点法”作出它在一个周期内的图象;
(3)说明y=2sin
 的图象可由y=sinx的图象经过怎样的变换而得到.
的图象可由y=sinx的图象经过怎样的变换而得到.(1)振幅A=2,周期T=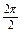 =
=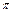 ,初相
,初相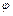 =
=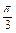 .(2)图象见解析(3)把y=sinx的图象上所有的点向左平移
.(2)图象见解析(3)把y=sinx的图象上所有的点向左平移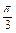 个单位,得到y=sin
个单位,得到y=sin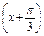 的图象,再把y=sin
的图象,再把y=sin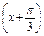 的图象上的点的横坐标缩短到原来的
的图象上的点的横坐标缩短到原来的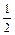 倍(纵坐标不变),得到y=sin
倍(纵坐标不变),得到y=sin 的图象,最后把y=sin
的图象,最后把y=sin 上所有点的纵坐标伸长到原来的2倍(横坐标不变),即可得到y=2sin
上所有点的纵坐标伸长到原来的2倍(横坐标不变),即可得到y=2sin 的图象.
的图象.
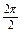 =
=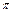 ,初相
,初相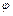 =
=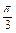 .(2)图象见解析(3)把y=sinx的图象上所有的点向左平移
.(2)图象见解析(3)把y=sinx的图象上所有的点向左平移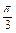 个单位,得到y=sin
个单位,得到y=sin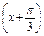 的图象,再把y=sin
的图象,再把y=sin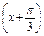 的图象上的点的横坐标缩短到原来的
的图象上的点的横坐标缩短到原来的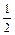 倍(纵坐标不变),得到y=sin
倍(纵坐标不变),得到y=sin 的图象,最后把y=sin
的图象,最后把y=sin 上所有点的纵坐标伸长到原来的2倍(横坐标不变),即可得到y=2sin
上所有点的纵坐标伸长到原来的2倍(横坐标不变),即可得到y=2sin 的图象.
的图象.(1)y=2sin 的振幅A=2,周期T=
的振幅A=2,周期T=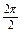 =
=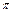 ,初相
,初相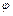 =
=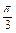 .
.
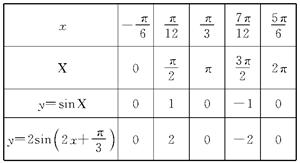
(2)令X=2x+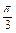 ,则y=2sin
,则y=2sin =2sinX.
=2sinX.
列表,并描点画出图象:
(3)方法一 把y=sinx的图象上所有的点向左平移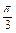 个单位,得到y=sin
个单位,得到y=sin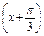 的图象,再把y=sin
的图象,再把y=sin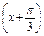 的图象上的点的横坐标缩短到原来的
的图象上的点的横坐标缩短到原来的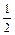 倍(纵坐标不变),得到y=sin
倍(纵坐标不变),得到y=sin 的图象,最后把y=sin
的图象,最后把y=sin 上所有点的纵坐标伸长到原来的2倍(横坐标不变),即可得到y=2sin
上所有点的纵坐标伸长到原来的2倍(横坐标不变),即可得到y=2sin 的图象.
的图象.
方法二 将y=sinx的图象上每一点的横坐标x缩短为原来的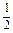 倍,纵坐标不变,得到y=sin2x的图象;
倍,纵坐标不变,得到y=sin2x的图象;
再将y=sin2x的图象向左平移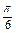 个单位;
个单位;
得到y=sin2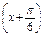 =sin
=sin 的图象;再将y=sin
的图象;再将y=sin 的图象上每一点的横坐标保持不变,纵坐标伸长为原来的2倍,得到y=2sin
的图象上每一点的横坐标保持不变,纵坐标伸长为原来的2倍,得到y=2sin 的图象.
的图象.
 的振幅A=2,周期T=
的振幅A=2,周期T=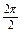 =
=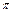 ,初相
,初相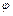 =
=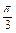 .
.

(2)令X=2x+
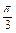 ,则y=2sin
,则y=2sin =2sinX.
=2sinX.列表,并描点画出图象:
(3)方法一 把y=sinx的图象上所有的点向左平移
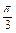 个单位,得到y=sin
个单位,得到y=sin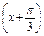 的图象,再把y=sin
的图象,再把y=sin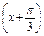 的图象上的点的横坐标缩短到原来的
的图象上的点的横坐标缩短到原来的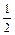 倍(纵坐标不变),得到y=sin
倍(纵坐标不变),得到y=sin 的图象,最后把y=sin
的图象,最后把y=sin 上所有点的纵坐标伸长到原来的2倍(横坐标不变),即可得到y=2sin
上所有点的纵坐标伸长到原来的2倍(横坐标不变),即可得到y=2sin 的图象.
的图象.方法二 将y=sinx的图象上每一点的横坐标x缩短为原来的
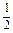 倍,纵坐标不变,得到y=sin2x的图象;
倍,纵坐标不变,得到y=sin2x的图象;再将y=sin2x的图象向左平移
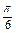 个单位;
个单位;得到y=sin2
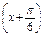 =sin
=sin 的图象;再将y=sin
的图象;再将y=sin 的图象上每一点的横坐标保持不变,纵坐标伸长为原来的2倍,得到y=2sin
的图象上每一点的横坐标保持不变,纵坐标伸长为原来的2倍,得到y=2sin 的图象.
的图象.
练习册系列答案
相关题目
 (a∈(0,1)),求f(x)的最值,并讨论周期性,奇偶性,单调性。
(a∈(0,1)),求f(x)的最值,并讨论周期性,奇偶性,单调性。 的最小正周期为 ,此函数的值域为 。
的最小正周期为 ,此函数的值域为 。 的部分图象如图,则( )
的部分图象如图,则( ) ;
; ;
;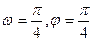 ;
;

 +
+ )的图像,请写出变换过程,并画出一个周期的闭区间的函数简图
)的图像,请写出变换过程,并画出一个周期的闭区间的函数简图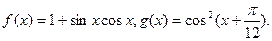
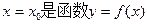 图象的一条对称轴,求
图象的一条对称轴,求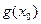 的值;
的值;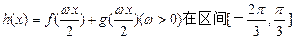 上是增函数的
上是增函数的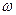 的最大值.
的最大值.  是( )
是( )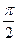 的偶函数
的偶函数 的非奇非偶函数
的非奇非偶函数 的最大值为
的最大值为 ,周期为
,周期为 ,且它的图象经过点
,且它的图象经过点 ,求函数的解析式.
,求函数的解析式.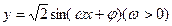 的初相和频率分别为
的初相和频率分别为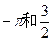 ,则它的相位是 .
,则它的相位是 .