题目内容
已知函数 (a∈(0,1)),求f(x)的最值,并讨论周期性,奇偶性,单调性。
(a∈(0,1)),求f(x)的最值,并讨论周期性,奇偶性,单调性。
 (a∈(0,1)),求f(x)的最值,并讨论周期性,奇偶性,单调性。
(a∈(0,1)),求f(x)的最值,并讨论周期性,奇偶性,单调性。见解析
:对三角函数式降幂
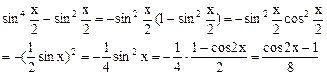
∴ f(x)=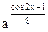 令
令  则 y=au∴ 0<a<1∴ y=au是减函数
则 y=au∴ 0<a<1∴ y=au是减函数
∴ 由 得
得 ,此为f(x)的减区间
,此为f(x)的减区间
由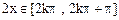 得
得 ,此为f(x)增区间
,此为f(x)增区间
∵ u(-x)=u(x)∴ f(x)=f(-x)∴ f(x)为偶函数∵ u(x+π)=f(x)
∴ f(x+π)=f(x)∴ f(x)为周期函数,最小正周期为π
当x=kπ(k∈Z)时,ymin=1当x=kπ+ (k∈Z)时,ynax=
(k∈Z)时,ynax=
注:研究三角函数性质,一般降幂化为y=Asin(ωx+φ)等一名一次一项的形式。
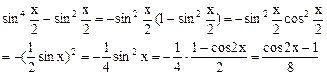
∴ f(x)=
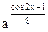 令
令  则 y=au∴ 0<a<1∴ y=au是减函数
则 y=au∴ 0<a<1∴ y=au是减函数∴ 由
 得
得 ,此为f(x)的减区间
,此为f(x)的减区间由
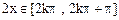 得
得 ,此为f(x)增区间
,此为f(x)增区间∵ u(-x)=u(x)∴ f(x)=f(-x)∴ f(x)为偶函数∵ u(x+π)=f(x)
∴ f(x+π)=f(x)∴ f(x)为周期函数,最小正周期为π
当x=kπ(k∈Z)时,ymin=1当x=kπ+
 (k∈Z)时,ynax=
(k∈Z)时,ynax=
注:研究三角函数性质,一般降幂化为y=Asin(ωx+φ)等一名一次一项的形式。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, 。
。 时,求函数f(x)的最大值、最小值。
时,求函数f(x)的最大值、最小值。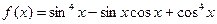 ,则
,则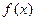 的值域是 。
的值域是 。 的部分图象如图所示,则
的部分图象如图所示,则 =( )
=( )



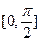 上为减函数的是
上为减函数的是
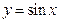


 ,求
,求 的值.
的值. 的图像,只需将函数
的图像,只需将函数 图像上所有的点( )
图像上所有的点( ) 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移 个单位长度
个单位长度 个单位长度
个单位长度