题目内容
对于集合M,N,定义M-N={x|x∈M,且x∉N},M⊕N=(M-N)∪(N-M),设A={x|x≥-
},B={x|x<0},则A⊕B=
| 9 |
| 4 |
{x|x≥0或x<-
}
| 9 |
| 4 |
{x|x≥0或x<-
}
.| 9 |
| 4 |
分析:根据定义,先求出A-B和B-A,然后利用M⊕N的定义求A⊕B即可.
解答: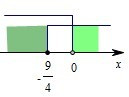 解:∵A={x|x≥-
解:∵A={x|x≥-
},B={x|x<0},
∴A-B={x|x≥-
且x≥0}={x|x≥0},B-A={x|x<-
且x<0}={x|x<-
},
∴A⊕B={x|x≥0}∪{x|x<-
}={x|x≥0或x<-
}.
故答案为:{x|x≥0或x<-
}.
 解:∵A={x|x≥-
解:∵A={x|x≥-| 9 |
| 4 |
∴A-B={x|x≥-
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
∴A⊕B={x|x≥0}∪{x|x<-
| 9 |
| 4 |
| 9 |
| 4 |
故答案为:{x|x≥0或x<-
| 9 |
| 4 |
点评:本题主要考查集合新定义的应用以及集合的基本运算,利用数轴是解决此类问题的基本方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
对于集合M、N,定义M-N={x|x∈M,且x∉N},M△N=(M-N)∪(N-M),设A={t|t=x2-3x,x∈R},B={x|y=lg(-x)},则A△B=( )
A、(-
| ||
B、[-
| ||
C、(-∞,-
| ||
D、(-∞,-
|