题目内容
 已知函数f(x)=x2-2x-3.
已知函数f(x)=x2-2x-3.(1)求f(x)的值域;
(2)f(x)的图象与x轴有两个交点,求出这两个交点的坐标;
(3)求使函数值为正时的x的取值范围;
(4)在右侧的坐标系中,作出函数y=|x2-2|x|-3|的图象.
分析:(1)将二次函数进行配方的函数的值域.
(2)由f(x)=0,可的交点坐标.
(3)解不等式f(x)>0即可.
(4)利用函数奇偶性作出函数的图象.
(2)由f(x)=0,可的交点坐标.
(3)解不等式f(x)>0即可.
(4)利用函数奇偶性作出函数的图象.
解答:解:(1)f(x)=x2-2x-3=(x-1)2-4≥-4,所以y≥-4,即函数的值域为{y|y≥-4}.
(2)要使f(x)的图象与x轴有两个交点,则由f(x)=x2-2x-3=0,解得x=3或x=-1,即这两个交点的坐标为(-1,0),(3,0).
(3)使函数值为正时,则f(x)=x2-2x-3>0,解得x>3或x<-1,即使函数值为正时的x的取值范围是x>3或x<-1.
(4)函数y=|x2-2|x|-3|的图象如图: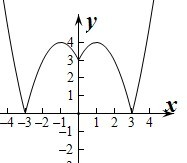
(2)要使f(x)的图象与x轴有两个交点,则由f(x)=x2-2x-3=0,解得x=3或x=-1,即这两个交点的坐标为(-1,0),(3,0).
(3)使函数值为正时,则f(x)=x2-2x-3>0,解得x>3或x<-1,即使函数值为正时的x的取值范围是x>3或x<-1.
(4)函数y=|x2-2|x|-3|的图象如图:

点评:本题主要考查二次函数的图象和性质,要求熟练掌握二次函数,二次方程以及二次不等式之间的关系.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|