题目内容
(本题满分13分)已知椭圆![]() 经过点(0,
经过点(0,![]() ),离心率为
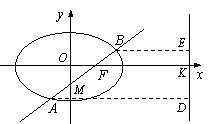
),离心率为![]() ,直线l经过椭圆C的右焦点F交椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
,直线l经过椭圆C的右焦点F交椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l交y轴于点M,且![]() ,当直线l的倾斜角变化时,探求
,当直线l的倾斜角变化时,探求![]() 的值是否为定值?若是,求出
的值是否为定值?若是,求出![]() 的值,否则,说明理由;
的值,否则,说明理由;
(Ⅲ)连接AE、BD,试探索当直线l的倾斜角变化时,直线AE与BD是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
解:(Ⅰ)依题意得b=![]() ,
,![]() ,
,![]() ,∴ a=2,c=1,
,∴ a=2,c=1,
∴ 椭圆C的方程![]() .…………………………………………………………3分
.…………………………………………………………3分
(Ⅱ)因直线l与y轴相交,故斜率存在,设直线l方程为:![]() ,求得l与y轴交于M(0,-k),又F坐标为 (1,0),设l交椭圆于
,求得l与y轴交于M(0,-k),又F坐标为 (1,0),设l交椭圆于![]() ,
,
 由
由 消去y得
消去y得![]() ,
,
![]() ,………5分
,………5分
又由 ![]() ∴
∴![]() ,
,
![]() 同理
同理![]() ,
,
![]() ,
,
![]()
![]() …………………7分
…………………7分
所以当直线l的倾斜角变化时,![]() 的值为定值
的值为定值![]() .………………………………8分
.………………………………8分
(Ⅲ)当直线l斜率不存在时,直线l⊥x轴,则![]() 为矩形,由对称性知,AE与BD相交于FK的中点
为矩形,由对称性知,AE与BD相交于FK的中点![]() ,
,
猜想,当直线l的倾斜角变化时,AE与BD相交于定点![]() ,…………………9分
,…………………9分
证明:由(Ⅱ)知![]() ,
,![]() ,
,
当直线l的倾斜角变化时,首先证直线AE过定点![]()
![]() ,
,
当![]() 时,
时,![]()
![]()
![]()
![]() . ………………………………11分
. ………………………………11分
∴点![]() 在直线
在直线![]() 上,同理可证,点
上,同理可证,点![]() 也在直线
也在直线![]() 上;
上;
∴当m变化时,AE与BD相交于定点![]() , …………………………………13分
, …………………………………13分

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
. 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 时,过点
时,过点 的直线
的直线 交曲线
交曲线 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合) 试问:直线
不重合) 试问:直线 与
与 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.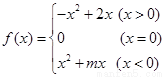 为奇函数;
为奇函数;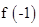 以及m的值;
以及m的值; 的图象;
的图象;
 有三个零点,求实数k的取值范围.
有三个零点,求实数k的取值范围.
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线
 取得最小值时点P的坐标.
取得最小值时点P的坐标.  是
是 轴上的动点,
轴上的动点, 分别切圆
分别切圆 于
于 两点
两点 ,求直线
,求直线 的方程;
的方程; 恒过一定点.
恒过一定点.