题目内容
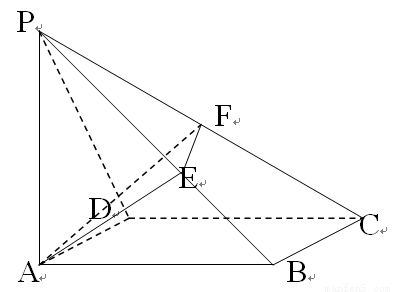
(本小题满分12分).如图所示,四棱锥P-ABCD,底面ABCD是边长为2的正方形,PA⊥面ABCD,PA=2,过点A作AE⊥PB,AF⊥PC,连接EF.
(1)求证:PC⊥面AEF.
(2)若面AEF交侧棱PD于点G(图中未标出点G),求多面体P—AEFG的体积。
【答案】
(1)证明: PA⊥面ABCD,BC在面内,∴ PA⊥BC
BA⊥BC,BC∩BA=B,∴BC⊥面PAB,又∵AE在面PAB内∴ BC⊥AE
PA⊥面ABCD,BC在面内,∴ PA⊥BC
BA⊥BC,BC∩BA=B,∴BC⊥面PAB,又∵AE在面PAB内∴ BC⊥AE AE⊥PB,BC∩PB=B, ,∴AE⊥面PBC又∵PC在面PBC内
AE⊥PB,BC∩PB=B, ,∴AE⊥面PBC又∵PC在面PBC内 AE⊥PC,
AE⊥PC,  AE⊥PC, AE∩AF=A, ∴PC⊥面AEF. ………5分
AE⊥PC, AE∩AF=A, ∴PC⊥面AEF. ………5分
(2)PC⊥面AEF, ∴ AG⊥PC,  AG⊥DC ∴PC∩DC=C AG⊥面PDC, ∵GF在面PDC内∴AG⊥GF
AG⊥DC ∴PC∩DC=C AG⊥面PDC, ∵GF在面PDC内∴AG⊥GF △AGF是直角三角形,由(1)可知△AEF是直角三角形,AE=AG=
△AGF是直角三角形,由(1)可知△AEF是直角三角形,AE=AG= ,EF=GF=
,EF=GF=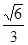 ∴
∴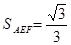 ,
,  又AF=
又AF=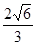 ,PF=
,PF=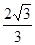 ∴
∴ ,∴
,∴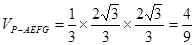 ………………12分
………………12分
【解析】略

练习册系列答案
相关题目