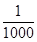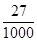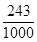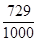题目内容
(本小题满分12分) 某居民小区有两个相互独立的安全防范系统(简称系统)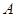 和
和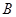 ,系统
,系统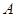 和
和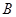 在任意时刻发生故障的概率分别为
在任意时刻发生故障的概率分别为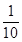 和
和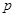 。
。
(Ⅰ)若在任意时刻至少有一个系统不发生故障的概率为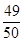 ,求
,求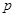 的值;
的值;
(Ⅱ)设系统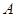 在3次相互独立的检测中不发生故障的次数为随机变量
在3次相互独立的检测中不发生故障的次数为随机变量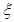 ,求
,求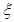 的概率分布列及数学期望
的概率分布列及数学期望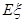 。
。
【答案】
(1)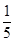 ;(2)E
;(2)E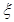 =0
=0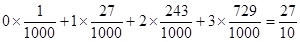 .
.
【解析】(1)设:“至少有一个系统不发生故障”为事件C,那么
1-P(C)=1-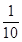 P=
P=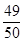 ,解得P=
,解得P=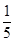 ………………………………4
分
………………………………4
分
(2)由题意,P(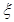 =0)=
=0)=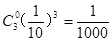 [来源:Z+xx+k.Com]
[来源:Z+xx+k.Com]
P(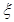 =1)=
=1)=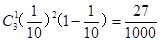
P(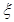 =2)=
=2)=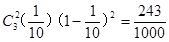
P(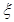 =3)=
=3)=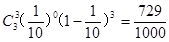
所以,随机变量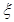 的概率分布列为:
的概率分布列为:
|
|
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
故随机变量X的数学期望为: E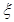 =0
=0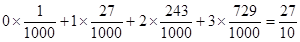 ……………………12分.
……………………12分.
[点评]本小题主要考查相互独立事件,独立重复试验、互斥事件、随机变量的分布列、数学期望等概念及相关计算,考查运用概率知识与方法解决实际问题的能力.

练习册系列答案
相关题目