题目内容
过原点0且方向向量为(m,1)的直线l与圆C:(x-1)2+y2=4相交于P、Q两点,则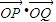 = .
= .
【答案】分析:本题为填空题,结果应该与m的取值无关,故可利用特值法,取m=0时,写出直线l的方程,与圆的方程联立,求出P、Q两点坐标,直接计算即可.
解答:解:特别的取m=0,此时直线l的方程为:x=0,代入圆的方程求得P(0,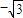 ),Q(0,
),Q(0,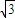 )
)
所以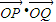 =-3.
=-3.
故答案为:-3
点评:本题考查直线的方向向量、直线与圆、及向量的数量积的运算,注意特值法在解题中的应用.
解答:解:特别的取m=0,此时直线l的方程为:x=0,代入圆的方程求得P(0,
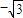 ),Q(0,
),Q(0,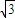 )
)所以
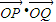 =-3.
=-3.故答案为:-3
点评:本题考查直线的方向向量、直线与圆、及向量的数量积的运算,注意特值法在解题中的应用.

练习册系列答案
相关题目
 =________.
=________. .
. 的直线l交双曲线C于A、B两点,求
的直线l交双曲线C于A、B两点,求 的值;
的值; 为常数.若存在,求出点P的坐标;若不存在,试说明理由.
为常数.若存在,求出点P的坐标;若不存在,试说明理由.