题目内容
已知线段MN的两个端点M、N分别在 轴、
轴、 轴上滑动,且
轴上滑动,且 ,点P在线段MN上,满足
,点P在线段MN上,满足
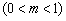 ,记点P的轨迹为曲线W.
,记点P的轨迹为曲线W.
(1)求曲线W的方程,并讨论W的形状与 的值的关系;
的值的关系;
(2)当 时,设A、B是曲线W与
时,设A、B是曲线W与 轴、
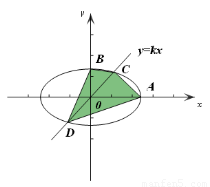
轴、 轴的正半轴的交点,过原点的直线与曲线W交于C、D两点,其中C在第一象限,求四边形ACBD面积的最大值.
轴的正半轴的交点,过原点的直线与曲线W交于C、D两点,其中C在第一象限,求四边形ACBD面积的最大值.
【答案】
(1)当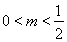 时,曲线
时,曲线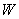 的方程为
的方程为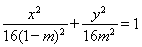 ,表示焦点在
,表示焦点在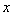 轴上的椭圆;当
轴上的椭圆;当 时,曲线
时,曲线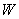 的方程为
的方程为 ,
,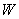 为以原点为圆心、半径为2的圆;当
为以原点为圆心、半径为2的圆;当 时,曲线
时,曲线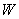 的方程为
的方程为 ,表示焦点在
,表示焦点在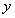 轴上的椭圆.(2)
轴上的椭圆.(2) .
.
【解析】
试题分析:(1)设出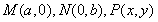 ,根据已知条件
,根据已知条件 以及
以及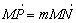
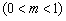 ,得到一个关系式
,得到一个关系式 ,化简成标准形式为
,化简成标准形式为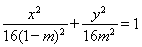 ,分别讨论当
,分别讨论当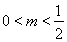 ,
, ,
, 时所表达的
时所表达的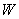 的形状;(2)由
的形状;(2)由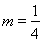 ,则曲线
,则曲线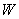 的方程是
的方程是 ,得出
,得出 ,再设
,再设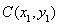
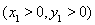 ,依据对称性得
,依据对称性得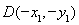 ,表示出
,表示出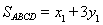 ,根据基本不等式得到
,根据基本不等式得到 ,故四边形
,故四边形 面积有最大值
面积有最大值 .
.
试题解析:(1)设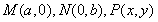 ,则
,则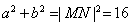 ,而由
,而由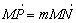
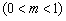 ,则
,则 ,解得
,解得 ,代入得:
,代入得: ,化简得
,化简得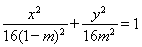 .
.
当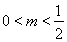 时,曲线
时,曲线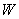 的方程为
的方程为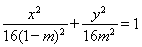 ,表示焦点在
,表示焦点在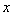 轴上的椭圆;
轴上的椭圆;
当 时,曲线
时,曲线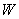 的方程为
的方程为 ,
,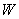 为以原点为圆心、半径为2的圆;
为以原点为圆心、半径为2的圆;
当 时,曲线
时,曲线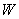 的方程为
的方程为 ,表示焦点在
,表示焦点在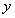 轴上的椭圆.
轴上的椭圆.
(2)由(1)当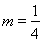 时,曲线
时,曲线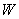 的方程是
的方程是 ,可得
,可得 .设
.设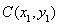
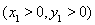 ,由对称性可得
,由对称性可得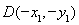 .因此,四边形
.因此,四边形 的面积
的面积 ,
,
即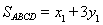 ,而
,而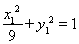 ,即
,即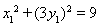 ,所以四边形
,所以四边形 的面积
的面积 当且仅当
当且仅当 时,即
时,即 且
且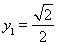 时取等号,故当C的坐标为
时取等号,故当C的坐标为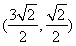 时,四边形
时,四边形 面积有最大值
面积有最大值 .
.
考点:1.椭圆的标准方程;2.直线与圆锥曲线的联立问题.

练习册系列答案
相关题目
 =m
=m (0<m<1),记点P的轨迹为曲线W.
(0<m<1),记点P的轨迹为曲线W. 时,设A、B是曲线W与x轴、y轴的正半轴的交点,过原点的直线与曲线W交于C、D两点,其中C在第一象限,求四边形ACBD面积的最大值.
时,设A、B是曲线W与x轴、y轴的正半轴的交点,过原点的直线与曲线W交于C、D两点,其中C在第一象限,求四边形ACBD面积的最大值.