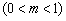题目内容
已知线段MN的两个端点M、N分别在x轴、y轴上滑动,且|MN|=4,点P在线段MN上,满足 =m
=m (0<m<1),记点P的轨迹为曲线W.
(0<m<1),记点P的轨迹为曲线W.(1)求曲线W的方程,并讨论W的形状与m的值的关系;
(2)当m=
 时,设A、B是曲线W与x轴、y轴的正半轴的交点,过原点的直线与曲线W交于C、D两点,其中C在第一象限,求四边形ACBD面积的最大值.
时,设A、B是曲线W与x轴、y轴的正半轴的交点,过原点的直线与曲线W交于C、D两点,其中C在第一象限,求四边形ACBD面积的最大值.
【答案】分析:(1)设M(a,0)、N(0,b)、P(x,y),根据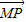 =m
=m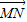 的坐标关系列式,解出用x、y表示a、b的式子,结合a2+b2=16代入并化简整理即可得到曲线W的方程为
的坐标关系列式,解出用x、y表示a、b的式子,结合a2+b2=16代入并化简整理即可得到曲线W的方程为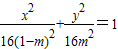 .再根据m值与
.再根据m值与 的大小关系进行讨论,即可得到各种情况下曲线W的形状;
的大小关系进行讨论,即可得到各种情况下曲线W的形状;
(2)由(1)得当m= 时,曲线W表示椭圆:
时,曲线W表示椭圆: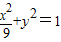 ,可得A、B两点的坐标.设C(x1,y1),D(-x1,-y1),结合图形将四边形ACBD面积表示成四个三角形面积之和,代入数据得到S四边形ACBD=x1+3y1,最后根据椭圆方程并利用基本不等式,算出当且仅当x1=
,可得A、B两点的坐标.设C(x1,y1),D(-x1,-y1),结合图形将四边形ACBD面积表示成四个三角形面积之和,代入数据得到S四边形ACBD=x1+3y1,最后根据椭圆方程并利用基本不等式,算出当且仅当x1=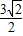 且y1=
且y1=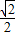 时,四边形ABCD面积有最大值3
时,四边形ABCD面积有最大值3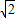 .
.
解答:解:(1)设M(a,0),N(0,b),P(x,y),则a2+b2=|MN|2=16,
而由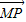 =m
=m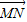 有:(x-a,y)=m(-a,b),解得:
有:(x-a,y)=m(-a,b),解得: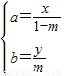 ,代入得:
,代入得: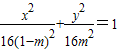 .
.
当0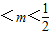 时,曲线W的方程为
时,曲线W的方程为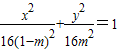 ,表示焦点在x轴上的椭圆;
,表示焦点在x轴上的椭圆;
当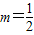 时,曲线W的方程为x2+y2=4,W为以原点为圆心、半径为2的圆;
时,曲线W的方程为x2+y2=4,W为以原点为圆心、半径为2的圆;
当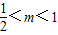 时,曲线W的方程为
时,曲线W的方程为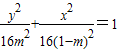 ,表示焦点在y轴上的椭圆.
,表示焦点在y轴上的椭圆.
(2)由(1)当m= 时,曲线W的方程是
时,曲线W的方程是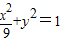 ,可得A(3,0),B(0,1).
,可得A(3,0),B(0,1).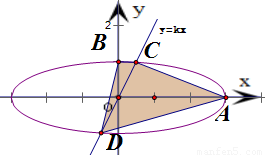
设C(x1,y1),则x1>0,y1>0,
由对称性可得D(-x1,-y1).
因此,S四边形ACBD=S△BOC+S△BOD+S△AOC+S△AOD
= |BO|(x1+x1)+
|BO|(x1+x1)+ |AO|(y1+y1),
|AO|(y1+y1),
即S四边形ACBD=x1+3y1,而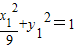 ,即
,即 ,
,
所以S四边形ACBD=x1+3y1≤2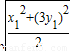 =3
=3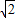
当且仅当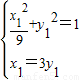 时,即x1=
时,即x1=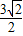 且y1=
且y1=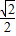 时取等号,
时取等号,
故当C的坐标为(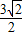 ,
,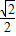 )时,四边形ABCD面积有最大值3
)时,四边形ABCD面积有最大值3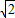
点评:本题给出动点P,求点P的轨迹方程并讨论相应曲线的形状,探索了四边形面积的最大值.着重考查了轨迹方程的求法、椭圆的简单几何性质和基本不等式求最值等知识,属于中档题.
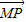 =m
=m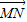 的坐标关系列式,解出用x、y表示a、b的式子,结合a2+b2=16代入并化简整理即可得到曲线W的方程为
的坐标关系列式,解出用x、y表示a、b的式子,结合a2+b2=16代入并化简整理即可得到曲线W的方程为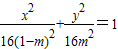 .再根据m值与
.再根据m值与 的大小关系进行讨论,即可得到各种情况下曲线W的形状;
的大小关系进行讨论,即可得到各种情况下曲线W的形状;(2)由(1)得当m=
 时,曲线W表示椭圆:
时,曲线W表示椭圆: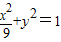 ,可得A、B两点的坐标.设C(x1,y1),D(-x1,-y1),结合图形将四边形ACBD面积表示成四个三角形面积之和,代入数据得到S四边形ACBD=x1+3y1,最后根据椭圆方程并利用基本不等式,算出当且仅当x1=
,可得A、B两点的坐标.设C(x1,y1),D(-x1,-y1),结合图形将四边形ACBD面积表示成四个三角形面积之和,代入数据得到S四边形ACBD=x1+3y1,最后根据椭圆方程并利用基本不等式,算出当且仅当x1=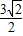 且y1=
且y1=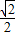 时,四边形ABCD面积有最大值3
时,四边形ABCD面积有最大值3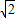 .
.解答:解:(1)设M(a,0),N(0,b),P(x,y),则a2+b2=|MN|2=16,
而由
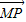 =m
=m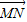 有:(x-a,y)=m(-a,b),解得:
有:(x-a,y)=m(-a,b),解得: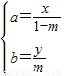 ,代入得:
,代入得: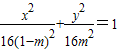 .
.当0
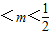 时,曲线W的方程为
时,曲线W的方程为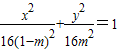 ,表示焦点在x轴上的椭圆;
,表示焦点在x轴上的椭圆;当
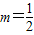 时,曲线W的方程为x2+y2=4,W为以原点为圆心、半径为2的圆;
时,曲线W的方程为x2+y2=4,W为以原点为圆心、半径为2的圆;当
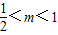 时,曲线W的方程为
时,曲线W的方程为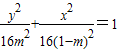 ,表示焦点在y轴上的椭圆.
,表示焦点在y轴上的椭圆.(2)由(1)当m=
 时,曲线W的方程是
时,曲线W的方程是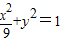 ,可得A(3,0),B(0,1).
,可得A(3,0),B(0,1).
设C(x1,y1),则x1>0,y1>0,
由对称性可得D(-x1,-y1).
因此,S四边形ACBD=S△BOC+S△BOD+S△AOC+S△AOD
=
 |BO|(x1+x1)+
|BO|(x1+x1)+ |AO|(y1+y1),
|AO|(y1+y1),即S四边形ACBD=x1+3y1,而
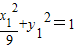 ,即
,即 ,
,所以S四边形ACBD=x1+3y1≤2
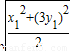 =3
=3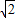
当且仅当
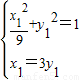 时,即x1=
时,即x1=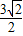 且y1=
且y1=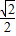 时取等号,
时取等号,故当C的坐标为(
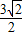 ,
,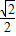 )时,四边形ABCD面积有最大值3
)时,四边形ABCD面积有最大值3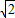
点评:本题给出动点P,求点P的轨迹方程并讨论相应曲线的形状,探索了四边形面积的最大值.着重考查了轨迹方程的求法、椭圆的简单几何性质和基本不等式求最值等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目