题目内容

（07年北师大附中） 设函数y = x3 + ax2 + bx + c的图象如图所示，且与y = 0在原点相切，若函数的极小值为－4，

（1）求a、b、c的值；（2）求函数的递减区间。

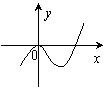
解析：（1）函数的图象经过（0，0）点

∴ c = 0，又图象与x轴相切于（0，0）点，= 3x2 + 2ax + b.

∴ 0 = 3×02 + 2a×0 + b，得b = 0

∴ y = x3 + ax2，= 3x2 + 2ax.

当x＜a时，＜0；x＞a时，＞0，

当x = a时，函数有极小值－4.

∴ ，得a = －3

（2）=3x2－6x＜0，解得0＜x＜2，∴ 递减区间是（0，2）

练习册系列答案
相关题目

（07年北师大附中） 已知函数f (x ) = kx3－3 (k +1) x2－k2 + 1（k＞0）.

（1）若f (x )的单调减区间为(0，4)，求k的值；

（2）当x＞k时，求证：2＞3－.

（07年北师大附中） 设抛物线y = 4－x2与直线y =3x的交点为A、B，点M在抛物线的AB弧上运动，设达到最大值时，点M的坐标为(p，h)

（1）过点(p，h)的切线方程；

 

（07年北师大附中） 已知f (x ) = x3 + bx2 + cx + d在(－∞，0)上是增函数，在[0，2]上是减函数，且方程f (x ) = 0有三个根，它们分别为α，2，β.

（1）求c的值；

（2）求证：f (1 )≥2.

（07年北师大附中）  已知函数f (x ) = x4－4x3 + ax2－1在区间[0，1]单调递增，在区间[1，2单调递减.

（1）求a的值；

（2）若点A (x0，f (x0))在函数f (x )的图像上，求证点A关于直线x = 1的对称点B也在函数f (x )的图像上；

（3）是否存在实数b，使得函数g (x ) = bx2－1的图像与函数f (x )的图像恰有3个交点，若存在，请求出实数b的值；若不存在，试说明理由.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网