题目内容
设a是正数,ax+y=2(x≥0,y≥0),记y+3x- x2的最大值是M(a),试求:
x2的最大值是M(a),试求:(1)M(a)的表达式;(2)M(a)的最小值.
【答案】分析:(1)将代数式y+3x- x2表示为一个字母,由ax+y=2解出y后代入消元,建立关于x的二次函数,逐步进行分类求M(a).
x2表示为一个字母,由ax+y=2解出y后代入消元,建立关于x的二次函数,逐步进行分类求M(a).
(2)由(1)知)M(a)是分段函数,对每一段进行求最小值,然后从中选最小的,作为M(a)的最小值.
解答:解:(1)设S(x)=y+3x- x2,将y=2-ax代入消去y,得:
x2,将y=2-ax代入消去y,得:
S(x)=2-ax+3x- x2
x2
=- x2+(3-a)x+2
x2+(3-a)x+2
=- [x-(3-a)]2+
[x-(3-a)]2+ (3-a)2+2(x≥0)
(3-a)2+2(x≥0)
∵y≥0∴2-ax≥0
而a>0∴0≤x≤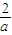
下面分三种情况求M(a)
(i)当0<3-a<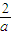 (a>0),即
(a>0),即
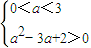 时
时
解得0<a<1或2<a<3时
M(a)=S(3-a)= (3-a)2+2
(3-a)2+2
(ii)当3-a≥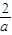 (a>0)即
(a>0)即
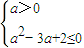 时,
时,
解得:1≤a≤2,这时
M(a)=S(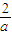 )=2-a•+3•
)=2-a•+3•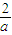 -
- •
•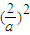 =-
=-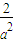 +
+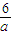
(iii)当3-a≤0;即a≥3时
M(a)=S(0)=2
综上所述得:
M(a)=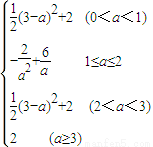
(2)下面分情况探讨M(a)的最小值.
当0<a<1或2<a<3时
M(a)= (3-a)2+2>2
(3-a)2+2>2
当1≤a≤2时
M(a)=-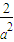 +
+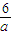 =-2(
=-2( -
- )2+
)2+
∵1≤a≤2⇒ ≤
≤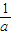 ≤1
≤1
∴当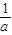 =
= 时,M(a)取小值,即
时,M(a)取小值,即
M(a)≥M(2)=
当a≥3时,M(a)=2
经过比较上述各类中M(a)的最小者,可得M(a)的最小值是2.
点评:本题主要考查函数思想的和分类讨论思想.解题经验的积累,有利于解题思路的挖掘,对参数a的分类,完全依据二次函数顶点的横坐标3-a是否在定义域区间[0,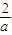 ]内,这样就引出三种讨论情况,找出解题的方案.
]内,这样就引出三种讨论情况,找出解题的方案.
 x2表示为一个字母,由ax+y=2解出y后代入消元,建立关于x的二次函数,逐步进行分类求M(a).
x2表示为一个字母,由ax+y=2解出y后代入消元,建立关于x的二次函数,逐步进行分类求M(a).(2)由(1)知)M(a)是分段函数,对每一段进行求最小值,然后从中选最小的,作为M(a)的最小值.
解答:解:(1)设S(x)=y+3x-
 x2,将y=2-ax代入消去y,得:
x2,将y=2-ax代入消去y,得:S(x)=2-ax+3x-
 x2
x2=-
 x2+(3-a)x+2
x2+(3-a)x+2=-
 [x-(3-a)]2+
[x-(3-a)]2+ (3-a)2+2(x≥0)
(3-a)2+2(x≥0)∵y≥0∴2-ax≥0
而a>0∴0≤x≤
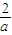
下面分三种情况求M(a)
(i)当0<3-a<
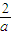 (a>0),即
(a>0),即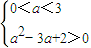 时
时解得0<a<1或2<a<3时
M(a)=S(3-a)=
 (3-a)2+2
(3-a)2+2(ii)当3-a≥
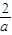 (a>0)即
(a>0)即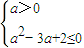 时,
时,解得:1≤a≤2,这时
M(a)=S(
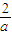 )=2-a•+3•
)=2-a•+3•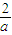 -
- •
•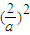 =-
=-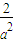 +
+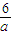
(iii)当3-a≤0;即a≥3时
M(a)=S(0)=2
综上所述得:
M(a)=
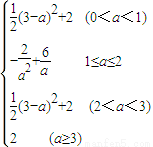
(2)下面分情况探讨M(a)的最小值.
当0<a<1或2<a<3时
M(a)=
 (3-a)2+2>2
(3-a)2+2>2当1≤a≤2时
M(a)=-
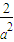 +
+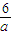 =-2(
=-2( -
- )2+
)2+
∵1≤a≤2⇒
 ≤
≤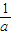 ≤1
≤1∴当
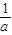 =
= 时,M(a)取小值,即
时,M(a)取小值,即M(a)≥M(2)=

当a≥3时,M(a)=2
经过比较上述各类中M(a)的最小者,可得M(a)的最小值是2.
点评:本题主要考查函数思想的和分类讨论思想.解题经验的积累,有利于解题思路的挖掘,对参数a的分类,完全依据二次函数顶点的横坐标3-a是否在定义域区间[0,
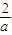 ]内,这样就引出三种讨论情况,找出解题的方案.
]内,这样就引出三种讨论情况,找出解题的方案. 
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目