题目内容
设a是正数,ax+y=2(x≥0,y≥0),记y+3x-![]() x2的最大值是M(a)。试求:
x2的最大值是M(a)。试求:
(1)M(a)的表达式;
(2)M(a)的最小值。
答案:
解析:
解析:
由ax十y=2解出y后代入y+3x- (1)设S(x)=y+3x- ∵y≥0,∴2-ax≥0 而a>0,∴0≤x≤ 下面分三种情况求M(a): ①当0<3-a< M(a)=S(3-a)= ②当3-a≥ ③当3-a≤0,即a≥3时,M(a)=S(0)。 综合以上,得 (2)下面分情况探讨M(a)的最小值。 当0<a<1或2<a<3时,M(a)= 当1≤a≤2时,M(a)= ∵1≤a≤2 ∴当 经比较上述各类中M(a)的最小者,可得M(a)的最小值是2。 |

练习册系列答案
相关题目
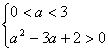 时解得0<a<1或2<a<3。这时
时解得0<a<1或2<a<3。这时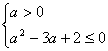 时,解得1≤a≤2,这时M(a),=S
时,解得1≤a≤2,这时M(a),=S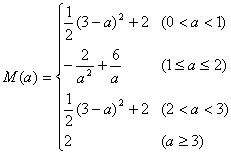
 x2的最大值是M(a),试求:
x2的最大值是M(a),试求: