题目内容
(本题满分12分)在数列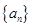 中,
中,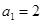 ,
,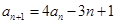 ,
, .
.
(1)证明数列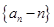 是等比数列;
是等比数列;
(2)设数列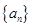 的前
的前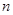 项和
项和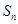 ,求
,求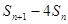 的最大值。
的最大值。
(1)由题设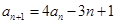 ,
,
得 ,
, .又
.又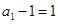 ,
,
所以数列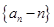 是首项为
是首项为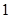 ,且公比为
,且公比为 的等比数列;(2)0.
的等比数列;(2)0.
解析试题分析:(Ⅰ)由题设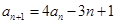 ,
,
得 ,
, .又
.又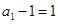 ,
,
所以数列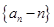 是首项为
是首项为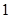 ,且公比为
,且公比为 的等比数列.…………4分
的等比数列.…………4分
(Ⅱ)由(Ⅰ)可知 ,于是数列
,于是数列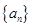 的通项公式为
的通项公式为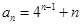 .……………6分
.……………6分
所以数列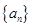 的前
的前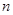 项和
项和 …8分
…8分
=  …………………10分
…………………10分
故当n=1时,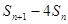 的最大值为0. …………………12分
的最大值为0. …………………12分
考点:等比数列的定义;等比数列的通项公式;数列前n项和的求法。
点评:在求数列的通项公式时,常用的一种方法是构造新数列,通过构造的新数列是等差数列或等比数列来求。

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
 是一个等差数列,
是一个等差数列,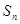 是其前
是其前 项和,且
项和,且 ,
, .
.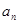 ;
; 的前10项的和
的前10项的和
 是等差数列,其中
是等差数列,其中 [来]
[来] 值。]
值。] ,
, 是
是 项和,且
项和,且 .
. 的通项公式;
的通项公式; ,
, 是
是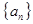 的前n项和,是否存在正数
的前n项和,是否存在正数 ,对任意正整数
,对任意正整数 ,不等式
,不等式 恒成立?若存在,求
恒成立?若存在,求 是否有解,说明理由;
是否有解,说明理由; ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。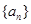 中,
中,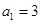 ,前
,前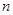 项和为
项和为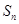 ,等比数列
,等比数列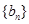 各项均为正数,
各项均为正数,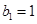 ,且
,且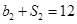 ,
,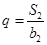 .
.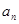 与
与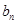 ;(2)求
;(2)求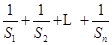 .
.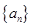 是等差数列,其前n项和公式为
是等差数列,其前n项和公式为 ,
,
 的值;
的值;  的前
的前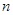 项和为
项和为 ,公差
,公差 
 成等比数列.
成等比数列.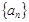 的通项公式;
的通项公式; 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列 的前
的前 .
.