题目内容
【题目】在平行四边形ABCD中,E,G分别是BC,DC上的点且 ![]() =3
=3 ![]() ,
, ![]() =3
=3 ![]() ,DE与BG交于点O.
,DE与BG交于点O. 
(1)求| ![]() |:|
|:| ![]() |;
|;
(2)若平行四边形ABCD的面积为21,求△BOC的面积.
【答案】
(1)解:由于D、O、E共线,故有 ![]() =λ
=λ ![]() =λ(
=λ( ![]() ﹣
﹣ ![]()
![]() ).
).
∵B、O、G共线,∴ ![]() =m
=m ![]() +(1﹣m)
+(1﹣m) ![]() =m(﹣
=m(﹣ ![]()
![]() )+(1﹣m)(
)+(1﹣m)( ![]() )
)
=﹣ ![]() m
m ![]() +(1﹣m)(
+(1﹣m)( ![]()
![]() ﹣
﹣ ![]()
![]() )=
)= ![]()
![]() +
+ ![]()
![]() ,
,
∴ ![]() =
= ![]()
![]() +
+ ![]()
![]() ,
,
∴λ( ![]() ﹣
﹣ ![]()
![]() )=
)= ![]()
![]() +
+ ![]()
![]() ,
,
∴ 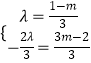 ,求得λ=
,求得λ= ![]() ,
,
可得| ![]() |:|
|:| ![]() |=
|= ![]()
(2)解:由(1)可得△BOC 与△BDC的高之比 ![]() =
= ![]() ,∴△BOC 与△BDC的面积之比为
,∴△BOC 与△BDC的面积之比为 ![]() =
= ![]() ,
,
∴S△BOC= ![]() S△BDC=
S△BDC= ![]()
![]() =
= ![]()
【解析】(1)由D、O、E共线,故有 ![]() =λ
=λ ![]() =λ(
=λ( ![]() ﹣
﹣ ![]()
![]() ).再由 B、O、G共线,求得
).再由 B、O、G共线,求得 ![]() =
= ![]()
![]() +
+ ![]()
![]() ,再利用平面向量基本定理求得λ 的值,即可得到结论.(2)由(1)可得
,再利用平面向量基本定理求得λ 的值,即可得到结论.(2)由(1)可得 ![]() =
= ![]() ,可得
,可得 ![]() =
= ![]() ,再根据S△BOC=
,再根据S△BOC= ![]() S△BDC , 计算求得结果.
S△BDC , 计算求得结果.
【考点精析】根据题目的已知条件,利用正弦定理的定义的相关知识可以得到问题的答案,需要掌握正弦定理:![]() .
.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
【题目】已知 ![]()
x | |||||
2x+ | |||||
sin(2x+ | |||||
f(x) |

(1)用五点法完成下列表格,并画出函数f(x)在区间 ![]() 上的简图;
上的简图;
(2)若 ![]() ,函数g(x)=f(x)+m的最小值为2,试求处函数g(x)的最大值,指出x取值时,函数g(x)取得最大值.
,函数g(x)=f(x)+m的最小值为2,试求处函数g(x)的最大值,指出x取值时,函数g(x)取得最大值.

