题目内容
已知a=sin ,b=cos
,b=cos ,c=tan
,c=tan ,则b、a、c的大小关 .
,则b、a、c的大小关 .
【答案】分析:注意到 互补,将a=sin
互补,将a=sin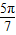 利用诱导公式化为 a=sin
利用诱导公式化为 a=sin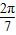 ,且
,且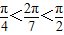 ,∴且a>b且均小于1,而c>1.大小关系即可确定.
,∴且a>b且均小于1,而c>1.大小关系即可确定.
解答:解:a=sin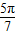 =sin(π-
=sin(π-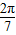 )=sin
)=sin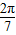 ,且
,且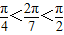 ∴sin
∴sin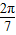 >cos
>cos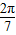 ,即1>a>b>0.又正切函数在(0,
,即1>a>b>0.又正切函数在(0,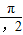 )上单调递增,∴c=tan
)上单调递增,∴c=tan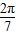 >tan
>tan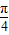 =1,
=1,
∴c>1>a>b>0.,
故答案为:c>a>b
点评:本题考查非特殊角三角函数值大小比较,可化为同角或同名函数再进行比较,用到的知识有同角三角函数基本关系式,三角函数的单调性.
 互补,将a=sin
互补,将a=sin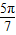 利用诱导公式化为 a=sin
利用诱导公式化为 a=sin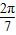 ,且
,且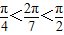 ,∴且a>b且均小于1,而c>1.大小关系即可确定.
,∴且a>b且均小于1,而c>1.大小关系即可确定.解答:解:a=sin
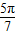 =sin(π-
=sin(π-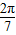 )=sin
)=sin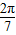 ,且
,且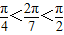 ∴sin
∴sin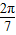 >cos
>cos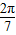 ,即1>a>b>0.又正切函数在(0,
,即1>a>b>0.又正切函数在(0,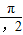 )上单调递增,∴c=tan
)上单调递增,∴c=tan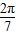 >tan
>tan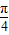 =1,
=1,∴c>1>a>b>0.,
故答案为:c>a>b
点评:本题考查非特殊角三角函数值大小比较,可化为同角或同名函数再进行比较,用到的知识有同角三角函数基本关系式,三角函数的单调性.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
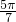 ,b=cos
,b=cos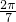 ,c=tan
,c=tan