题目内容

已知a=(sinα,cosα),b=(cosβ,sinβ)，b+c=(2cosβ,0),a·b=,a·c=,

求cos2(α+β)+tanα·cotβ的值.

解析:设c=(x,y),则b+c=(cosβ,sinβ)+(x,y)=(x+cosβ,y+sinβ)=(2cosβ,0),

∴∴

∴c=(cosβ,-sinβ).

∵a·b=,a·c=,

∴

∴

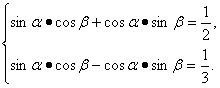
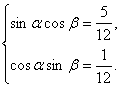
∴tanαcotβ=5.

又∵sin(α+β)=,

∴cos2(α+β)=1-2sin2(α+β)=.

∴cos2(α+β)+tanαcotβ=+5=.

练习册系列答案
相关题目
19、已知a=sin（-1），b=cos（-1），c=tan（-1），则a、b、c的大小关系是（　　）
已知
a
=(sinθ，1)，
b
=(1，cosθ)，
c
=(0，3)，-
π
2
＜θ＜
π
2
．
（1）若(4
a
-
c
)∥
b
，求θ；
（2）求|
a
+
b
|的取值范围．
下列命题：
（1）若函数f（x）=lg（x+
x2+a
），为奇函数，则a=1；
（2）函数f（x）=|sinx|的周期T=π；
（3）已知
a
=(sinθ，
1+cosθ
)，
b
=(1，
1-cosθ
)，其中θ∈（π，
3π
2
），则
a
⊥
b

（4）在△ABC中，
BA
=a，
AC
=b，若a•b＜0，则△ABC是钝角三角形
（ 5）O是△ABC所在平面上一定点，动点P满足：
OP
=
OA
+λ(
AB
sinC
+
AC
sinB
)，λ∈（0，+∞），则直线AP一定通过△ABC的内心．
以上命题为真命题的是
（1）（2）（3）（5）
（1）（2）（3）（5）
．
已知
a
=(sin(
π
4
+2α)，
6
6
)，
b
=(sin(
π
4
-2α)，-
6
6
)，α∈(
π
4
，
π
2
)，且
a
⊥
b
，求
2
sin2α+2cos2α的值．
已知
a
=(sinθ，cosθ)、
b
=(
3
，1)
（1）若
a
∥
b
，求tanθ的值；
（2）若f(θ)=|
a
+
b
|，△ABC的三条边分别为f（-
2π
3
）、f（-
π
6
）、f（
π
3
），求△ABC的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网