题目内容
在正项等差数列{an}中,对任意的n∈N*都有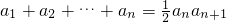 .
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}满足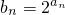 ,其前n项和为Sn,求证;对任意的n∈N*,Sn-bn+1均为定植.
,其前n项和为Sn,求证;对任意的n∈N*,Sn-bn+1均为定植.
(Ⅰ)解:在正项等差数列{an}中,
对任意的n∈N*都有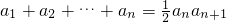 ,
,
令n=1,得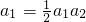 ,
,
∵a1>0,
∴a2=2.
令n=2,得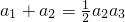 ,
,
即a1+2=a3=a1+2d,
故d=1.
∴an=2+(n-2)×1=n.
(Ⅱ)证明:∵an=n,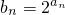 =2n,
=2n,
∴Sn=2+22+…+2n
=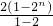
=2n+1-2.
故Sn-bn+1=(2n+1-2)-2n+1=-2,
∴对任意的n∈N*,Sn-bn+1均为定值-2.
分析:(Ⅰ)在正项等差数列{an}中,对任意的n∈N*都有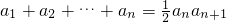 ,令n=1,得a2=2.令n=2,得d=1.由此能求出数列{an}的通项公式.
,令n=1,得a2=2.令n=2,得d=1.由此能求出数列{an}的通项公式.
(Ⅱ)由an=n,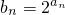 =2n,知Sn=2+22+…+2n=2n+1-2.故Sn-bn+1=(2n+1-2)-2n+1=-2,由此能够证明对任意的n∈N*,Sn-bn+1均为定值-2.
=2n,知Sn=2+22+…+2n=2n+1-2.故Sn-bn+1=(2n+1-2)-2n+1=-2,由此能够证明对任意的n∈N*,Sn-bn+1均为定值-2.
点评:本题考查数列的通项公式的求法和证明对任意的n∈N*,Sn-bn+1均为定值.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
对任意的n∈N*都有
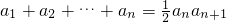 ,
,令n=1,得
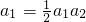 ,
,∵a1>0,
∴a2=2.
令n=2,得
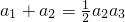 ,
,即a1+2=a3=a1+2d,
故d=1.
∴an=2+(n-2)×1=n.
(Ⅱ)证明:∵an=n,
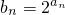 =2n,
=2n,∴Sn=2+22+…+2n
=
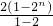
=2n+1-2.
故Sn-bn+1=(2n+1-2)-2n+1=-2,
∴对任意的n∈N*,Sn-bn+1均为定值-2.
分析:(Ⅰ)在正项等差数列{an}中,对任意的n∈N*都有
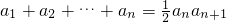 ,令n=1,得a2=2.令n=2,得d=1.由此能求出数列{an}的通项公式.
,令n=1,得a2=2.令n=2,得d=1.由此能求出数列{an}的通项公式.(Ⅱ)由an=n,
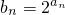 =2n,知Sn=2+22+…+2n=2n+1-2.故Sn-bn+1=(2n+1-2)-2n+1=-2,由此能够证明对任意的n∈N*,Sn-bn+1均为定值-2.
=2n,知Sn=2+22+…+2n=2n+1-2.故Sn-bn+1=(2n+1-2)-2n+1=-2,由此能够证明对任意的n∈N*,Sn-bn+1均为定值-2.点评:本题考查数列的通项公式的求法和证明对任意的n∈N*,Sn-bn+1均为定值.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
 anan+1。
anan+1。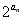 ,其前n项和为Sn,求Sn-bn+1的值。
,其前n项和为Sn,求Sn-bn+1的值。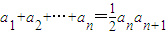 .
.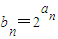 ,其前n项和为Sn,求证;对任意的n∈N*,Sn-bn+1均为定植.
,其前n项和为Sn,求证;对任意的n∈N*,Sn-bn+1均为定植.