题目内容
在正项等差数列{an}中,对任意的n∈N*都有a1+a2+…+an= anan+1。
anan+1。
(1)求数列{an}的通项an;
(2)设数列{bn}满足bn=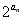 ,其前n项和为Sn,求Sn-bn+1的值。
,其前n项和为Sn,求Sn-bn+1的值。
 anan+1。
anan+1。(1)求数列{an}的通项an;
(2)设数列{bn}满足bn=
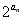 ,其前n项和为Sn,求Sn-bn+1的值。
,其前n项和为Sn,求Sn-bn+1的值。解:(1)由对任意的n∈N*都有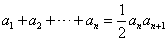
令n=1得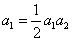
而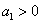 ,故
,故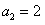
令 得
得
即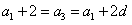
故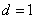
从而有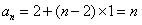 ;
;
(2)由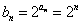 得
得

故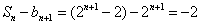 。
。
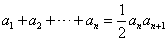
令n=1得
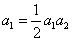
而
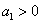 ,故
,故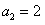
令
 得
得
即
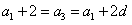
故
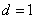
从而有
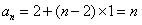 ;
;(2)由
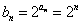 得
得
故
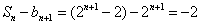 。
。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
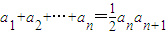 .
.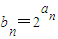 ,其前n项和为Sn,求证;对任意的n∈N*,Sn-bn+1均为定植.
,其前n项和为Sn,求证;对任意的n∈N*,Sn-bn+1均为定植.