题目内容
已知函数 f(x)的定义域为 ,其导函数f'(x)的图象如图所示,则对于任意x1,x2∈
,其导函数f'(x)的图象如图所示,则对于任意x1,x2∈ ( x1≠x2),下列结论正确的是
( x1≠x2),下列结论正确的是
①f(x)< 0恒成立;
②(x1-x2)[ f(x1)-f(x2)] < 0;
③(x1-x2)[ f(x1)-f(x2)] > 0;
④ >
>  ;
;
⑤ <
<  .
.
 ,其导函数f'(x)的图象如图所示,则对于任意x1,x2∈
,其导函数f'(x)的图象如图所示,则对于任意x1,x2∈ ( x1≠x2),下列结论正确的是
( x1≠x2),下列结论正确的是①f(x)< 0恒成立;
②(x1-x2)[ f(x1)-f(x2)] < 0;

③(x1-x2)[ f(x1)-f(x2)] > 0;
④
 >
>  ;
;⑤
 <
<  .
.| A.①③ | B.①③④ | C.②④ | D.②⑤ |
D
由图可得, 在定义域内恒成立,则
在定义域内恒成立,则 在定义域内单调递减。因为不确定
在定义域内单调递减。因为不确定 的正负情况,所以命题①无法确定。
的正负情况,所以命题①无法确定。
对任意 且
且 ,若
,若 ,则有
,则有 ,所以
,所以 ,若
,若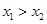 ,则有
,则有 ,所以
,所以 ,综上可得
,综上可得 ,故命题②正确,同理命题③不正确。
,故命题②正确,同理命题③不正确。
根据 的图象可知
的图象可知 在定义域内单调递增,所以
在定义域内单调递增,所以 是凹函数,所以
是凹函数,所以 ,故命题④不正确,命题⑤正确。
,故命题④不正确,命题⑤正确。
综上可得,选D。
 在定义域内恒成立,则
在定义域内恒成立,则 在定义域内单调递减。因为不确定
在定义域内单调递减。因为不确定 的正负情况,所以命题①无法确定。
的正负情况,所以命题①无法确定。对任意
 且
且 ,若
,若 ,则有
,则有 ,所以
,所以 ,若
,若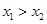 ,则有
,则有 ,所以
,所以 ,综上可得
,综上可得 ,故命题②正确,同理命题③不正确。
,故命题②正确,同理命题③不正确。根据
 的图象可知
的图象可知 在定义域内单调递增,所以
在定义域内单调递增,所以 是凹函数,所以
是凹函数,所以 ,故命题④不正确,命题⑤正确。
,故命题④不正确,命题⑤正确。综上可得,选D。

练习册系列答案
相关题目
 的零点的个数是( )
的零点的个数是( ) ,当
,当 且
且 时, 函数
时, 函数 的零点
的零点 ,则
,则 .
. 上的函数
上的函数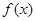 满足:
满足: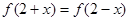 ,若方程
,若方程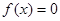 有且只有三个不等实根,且
有且只有三个不等实根,且 是其中之一,则方程的另外两个根为___________.
是其中之一,则方程的另外两个根为___________. 的零点是
的零点是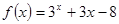 ,用二分法求方程
,用二分法求方程 内近似解的过程中得
内近似解的过程中得 则据此可得该方程的有解区间是
则据此可得该方程的有解区间是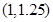
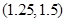
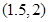
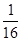 的解为( )
的解为( )