题目内容
（2012•浙江模拟）己知抛物线C：x2=2py（p＞0）上一点T（m，4）到其焦点的距离为| 17 |
| 4 |
（I）求p与m的值；
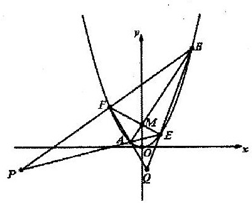
（II）如图，过点M（0，1）作两条直线l1，l2，ll与抛物线交于点A，B，l2与抛物线交于点E，F，且直线AE，BF交于点P，直线AF，BE交于点Q，求证：
| MP |
| MQ |
分析：（Ⅰ）由抛物线方程得其准线方程，进而根据抛物线定义可知点A（m，4）到焦点的距离等于它到准线的距离，求得p，则抛物线方程可得，把点A代入抛物线方程即可求得m．
（II）设直线l1的方程为y=kx+1，与抛物线方程联立，进而可得直线AE、BF；AF，BE的方程，从而可得P、Q的坐标，利用向量的数量积公式，即可得证．
（II）设直线l1的方程为y=kx+1，与抛物线方程联立，进而可得直线AE、BF；AF，BE的方程，从而可得P、Q的坐标，利用向量的数量积公式，即可得证．
解答：（Ⅰ）解：由抛物线方程得其准线方程：y=-
根据抛物线定义，点A（m，4）到焦点的距离等于它到准线的距离，
即4+
=
，解得p=
∴抛物线方程为：x2=y，
将A（m，4）代入抛物线方程可得m2=4，解得m=±2
（II）证明：直线l1的方程为y=kx+1，与抛物线方程联立，消去y可得x2-kx-1=0
设A（x1，x12），B（x2，x22），∴x1+x2=k，x1x2=-1
设E(x3，x32)，F(x4，x42)，则可得x3x4=-1
直线AE的斜率是kAE=x1+x3，方程为y=（x1+x3）x-x1x3
同理直线BF的方程为y=（x2+x4）x-x2x4
设P（m1，n1），则m1=
，n1=(x1+x3)×
-x1x3=-1
同理可得Q（
，-1）
∴
=（
，-2），
=（
，-2）
∴
•
=
×
+(-2)×(-2)=-1+4=3为定值．
| p |
| 2 |
根据抛物线定义，点A（m，4）到焦点的距离等于它到准线的距离，
即4+
| p |
| 2 |
| 17 |
| 4 |
| 1 |
| 2 |
∴抛物线方程为：x2=y，
将A（m，4）代入抛物线方程可得m2=4，解得m=±2
（II）证明：直线l1的方程为y=kx+1，与抛物线方程联立，消去y可得x2-kx-1=0
设A（x1，x12），B（x2，x22），∴x1+x2=k，x1x2=-1
设E(x3，x32)，F(x4，x42)，则可得x3x4=-1
直线AE的斜率是kAE=x1+x3，方程为y=（x1+x3）x-x1x3
同理直线BF的方程为y=（x2+x4）x-x2x4
设P（m1，n1），则m1=
| x1x3-x2x4 |
| x1+x3-x2-x4 |
| x1x3-x2x4 |
| x1+x3-x2-x4 |
同理可得Q（
| x1x4-x2x3 |
| x1+x4-x2-x3 |
∴
| MP |
| x1x3-x2x4 |
| x1+x3-x2-x4 |
| MQ |
| x1x4-x2x3 |
| x1+x4-x2-x3 |
∴
| MP |
| MQ |
| x1x3-x2x4 |
| x1+x3-x2-x4 |
| x1x4-x2x3 |
| x1+x4-x2-x3 |
点评：本题主要考查了抛物线的简单性质，考查抛物线的标准方程，考查直线与抛物线的位置关系，考查向量知识的运用，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
（2012•浙江模拟）将长方体截去一个四棱锥，得到的几何体如图所示，则该几何体的侧视图为（ ）