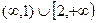题目内容
若不等式2x-1＞m(x2-1)对满足|m|≤2的所有m都成立，求x的取值范围.
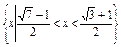
方法一 原不等式化为(x2-1)m-(2x-1)＜0.
令f(m)=(x2-1)m-(2x-1)(-2≤m≤2).
则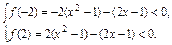
解得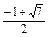
＜x＜
.
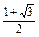方法二 求已知不等式视为关于m的不等式，
（1）若x2-1=0，即x=±1时，不等式变为2x-1＞0,即x＞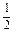
,∴x=1,此时原不等式恒成立.
（2）当x2-1＞0时，使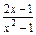
＞m对一切|m|≤2恒成立的充要条件是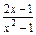＞2,
∴1＜x＜.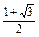
(3)当x2-1＜0时，使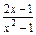＜m对一切|m|≤2恒成立的充要条件是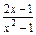＜-2.
∴
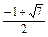＜x＜1.
由（1）（2）（3）知原不等式的解集为.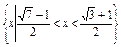
令f(m)=(x2-1)m-(2x-1)(-2≤m≤2).
则
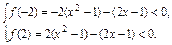
解得
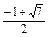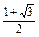＜x＜.方法二 求已知不等式视为关于m的不等式，
（1）若x2-1=0，即x=±1时，不等式变为2x-1＞0,即x＞
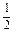,∴x=1,此时原不等式恒成立.（2）当x2-1＞0时，使
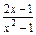＞m对一切|m|≤2恒成立的充要条件是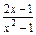＞2,∴1＜x＜
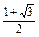.(3)当x2-1＜0时，使
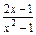＜m对一切|m|≤2恒成立的充要条件是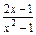＜-2.∴
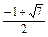＜x＜1.由（1）（2）（3）知原不等式的解集为
.
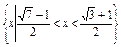练习册系列答案
阅读快车系列答案
相关题目
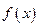是定义在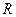
上的奇函数，当
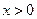时，
。
的解集。
的不等式
和
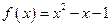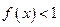的解集分别为
，
，求实数
的取值范围。(本题10分)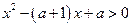
．
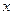的不等式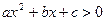
的解集是
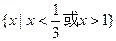，则关于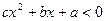
的解集为 ．
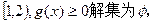则不等式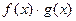
>0解集为（ ）
D 