题目内容
已知向量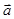 =(cosθ,sinθ),向量
=(cosθ,sinθ),向量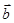 =(
=(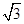 ,-1),则|2
,-1),则|2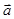 -
-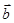 |的最大值与最小值的和是( )
|的最大值与最小值的和是( )
A.4 | B.6 | C.4 | D.16 |
C
解析试题分析:因为
|2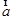 -
-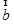 |
|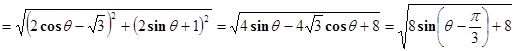 ,故其最大值为
,故其最大值为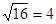 ,最小值为
,最小值为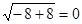 ,它们的和为
,它们的和为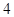 ,选C.
,选C.
考点:平面向量坐标运算、平面向量的模、两角差的正弦定理.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
已知向量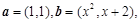 若
若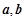 共线,则实数
共线,则实数 的值为( )
的值为( )
A.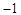 | B.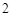 | C.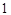 或 或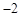 | D.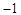 或 或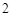 |
在 中,
中, 是边
是边 中点,角
中点,角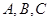 的对边分别是
的对边分别是 ,若
,若 ,则
,则 的形状为( )
的形状为( )
| A.等边三角形 | B.钝角三角形 |
| C.直角三角形 | D.等腰三角形但不是等边三角形. |
若等边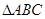 的边长为
的边长为 ,平面内一点
,平面内一点 满足
满足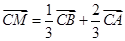 ,则
,则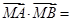 ( )
( )
A.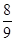 | B.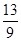 | C.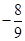 | D.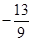 |
已知向量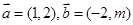 ,若
,若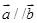 ,则
,则 等于( )
等于( )
A. | B.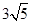 | C.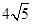 | D.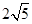 |
如果向量 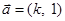 与
与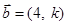 共线且方向相反,则
共线且方向相反,则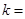 ( ).
( ).
A.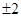 | B.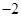 | C.2 | D.0 |
设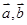 不共线,
不共线,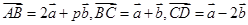 ,若
,若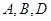 三点共线,则实数
三点共线,则实数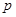 的值是: ( )
的值是: ( )
A.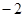 | B. | C.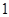 | D.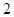 |
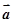 是已知的平面向量且
是已知的平面向量且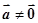 ,关于向量
,关于向量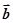 ,总存在向量
,总存在向量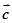 ,使
,使 ;
;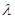 和
和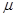 ,使
,使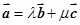 ;
; ⊥
⊥ ,则向量
,则向量
 ,
,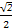 ,
, ,
,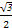 ,
,