题目内容
设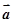 是已知的平面向量且
是已知的平面向量且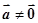 ,关于向量
,关于向量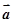 的分解,有如下四个命题:
的分解,有如下四个命题:
①给定向量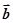 ,总存在向量
,总存在向量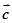 ,使
,使 ;
;
②给定向量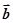 和
和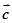 ,总存在实数
,总存在实数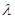 和
和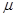 ,使
,使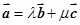 ;
;
③给定单位向量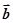 和正数
和正数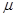 ,总存在单位向量
,总存在单位向量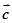 和实数
和实数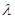 ,使
,使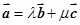 ;
;
④给定正数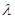 和
和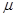 ,总存在单位向量
,总存在单位向量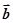 和单位向量
和单位向量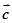 ,使
,使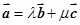 ;
;
上述命题中的向量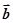 ,
,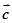 和
和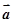 在同一平面内且两两不共线,则真命题的个数是( )
在同一平面内且两两不共线,则真命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
B.
解析试题分析:利用向量加法的三角形法则,易知①正确;利用平面向量的基本定理,易知正确;以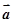 的终点作长度为
的终点作长度为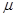 的圆,这个圆必须和向量
的圆,这个圆必须和向量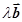 有交点,这个不一定能满足,故③是错的;利用向量加法的三角形法则,结合三角形两边的和大于第三边,即必须
有交点,这个不一定能满足,故③是错的;利用向量加法的三角形法则,结合三角形两边的和大于第三边,即必须 ,所以④是假命题。综上,本题选B.
,所以④是假命题。综上,本题选B.
考点:1.平面向量的基本定理;2.向量加法的平行四边形法则和三角形法则.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
在平面直角坐标系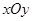 中,点
中,点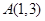 ,
,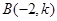 ,若向量
,若向量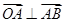 ,则实数
,则实数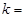 ( )
( )
A.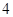 | B.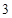 | C.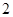 | D.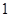 |
已知正方体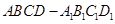 的棱长为
的棱长为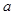 ,
,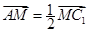 ,点N为
,点N为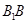 的中点, 则
的中点, 则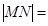 ( )
( )
A.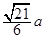 | B.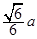 | C.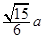 | D.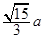 |
 、
、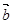 为平面向量,已知
为平面向量,已知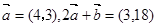 ,则
,则 、
、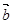 夹角的余弦值等于( ).
夹角的余弦值等于( ).
A.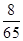 | B.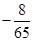 | C.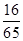 | D.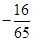 |
已知两个非零向量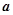 与
与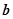 ,定义
,定义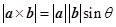 ,其中
,其中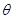 为
为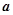 与
与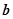 的夹角.若
的夹角.若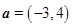 ,
, 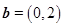 ,则
,则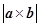 的值为 ( )
的值为 ( )
A.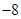 | B.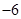 | C.8 | D.6 |
已知向量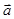 =(cosθ,sinθ),向量
=(cosθ,sinθ),向量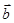 =(
=(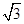 ,-1),则|2
,-1),则|2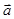 -
-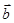 |的最大值与最小值的和是( )
|的最大值与最小值的和是( )
A.4 | B.6 | C.4 | D.16 |
已知向量 ,
,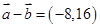 ,则
,则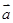 与
与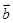 夹角的余弦值为( )
夹角的余弦值为( )
A.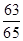 | B.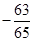 | C.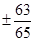 | D.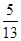 |
设点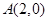 ,
,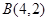 ,若点
,若点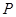 在直线
在直线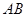 上,且
上,且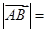
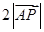 ,则点
,则点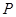 的坐标为( )
的坐标为( )
A.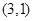 | B.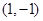 | C.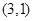 或 或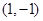 | D.无数多个 |
已知向量a=(1,m),b=(m,2),若a∥b,则实数m等于( )
A.- | B. |
C.- 或 或 | D.0 |