题目内容
已知函数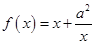 ,
,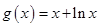 ,其中
,其中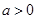 .
.
(1)若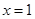 是函数
是函数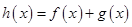 的极值点,求实数
的极值点,求实数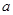 的值;
的值;
(2)若对任意的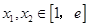 (
(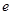 为自然对数的底数)都有
为自然对数的底数)都有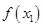 ≥
≥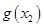 成立,求实数
成立,求实数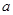 的取值范围.
的取值范围.
【解析】(1)根据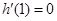 建立关于a的方程求a即可.
建立关于a的方程求a即可.
(2)本题要分别求出f(x)在[1,e]上的最小值,g(x)在[1,e]上的最大值,然后
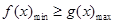 ,解关于a的不等式即可.
,解关于a的不等式即可.
【答案】
∵ ,其定义域为
,其定义域为 ,
,
∴ .
1分
.
1分
∵ 是函数
是函数 的极值点,∴
的极值点,∴ ,
2分
,
2分
即 .
3分
.
3分
∵ ,∴
,∴ .
4分
.
4分
(2)
对任意的 都有
都有 ≥
≥ 成立等价于对任意的
成立等价于对任意的
都有 ≥
≥ .
5分
.
5分
当
 [1,
[1, ]时,
]时, .
.
∴函数 在
在 上是增函数.
上是增函数.
∴ .
6分
.
6分
∵ ,且
,且 ,
, .
.
①当 且
且
 [1,
[1, ]时,
]时, ,
,
∴函数 在[1,
在[1, ]上是增函数,
]上是增函数,
∴ .
7分
.
7分
由 ≥
≥ ,得
,得 ≥
≥ ,又
,又 ,∴
,∴ 不合题意.
不合题意.
②当1≤ ≤
≤ 时,若1≤
时,若1≤ <
< ,则
,则 ,
,
若 <
< ≤
≤ ,则
,则 .
.
∴函数 在
在 上是减函数,在
上是减函数,在 上是增函数.
上是增函数.
∴ .
.
由 ≥
≥ ,得
,得 ≥
≥ ,又1≤
,又1≤ ≤
≤ ,∴
,∴ ≤
≤ ≤
≤ .
8分
.
8分
③当 且
且
 [1,
[1, ]时,
]时, ,
,
∴函数 在
在 上是减函数.∴
上是减函数.∴ .
.
由 ≥
≥ ,得
,得 ≥
≥ ,又
,又 ,∴
,∴ .
9分
.
9分
综上所述, 的取值范围为
的取值范围为 .
.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 ,函数
,函数 ,
, ,(其中e是自然对数的底数,为常数),
,(其中e是自然对数的底数,为常数), 时,求
时,求 的单调区间与极值;
的单调区间与极值; ,使得
,使得 ,
, .(其中
.(其中 为自然对数的底数),
为自然对数的底数), 在
在 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值;
的值; ≥0,
≥0, 恒成立,试确定实数
恒成立,试确定实数 时,是否存在实数
时,是否存在实数 ,使曲线C:
,使曲线C: 在点
在点
 轴垂直?若存在,求出
轴垂直?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. ,
, ,其中
,其中
 是函数
是函数 的极值点,求实数
的极值点,求实数 的值
的值 (
( 为自然对数的底数)都有
为自然对数的底数)都有 ≥
≥ 成立,求实数
成立,求实数 ,
, (其中
(其中 )的周期为π,且图象上一个最低点为
)的周期为π,且图象上一个最低点为 。
。 的解析式;
的解析式; 时,求
时,求