题目内容
13.已知等比数列{an}中,a1=3,a4=24.(1)求数列{an}的通项公式;
(2)若a3,a5分别是等差数列{bn}的第3项和第5项,试求数列{bn}的通项公式及其前n项和.
分析 (1)通过a1=3、a4=24可知公比q=2,进而可知数列{an}是以3为首项、2为公比的等比数列,计算即得结论;
(2)通过(1)可知a3=12、a5=48,进而可知数列{bn}是以-24为首项、18为公差等差数列,计算即得结论.
解答 解:(1)∵a1=3,a4=24,
∴q3=$\frac{{a}_{4}}{{a}_{1}}$=8,其中q为公比,
∴q=2,
∴数列{an}是以3为首项、2为公比的等比数列,
∴an=3•2n-1;
(2)由(1)可知a3=12,a5=48,
∴2d=a5-a3=36,即公差d=18,
∴首项a1=a3-2d=12-36=-24,
∴数列{bn}是以-24为首项、18为公差等差数列,
∴bn=-24+18(n-1)=18n-42,
数列{bn}的前n项和为$\frac{n(-24+18n-42)}{2}$=3n(3n-11).
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
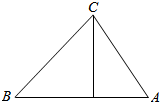 如图所示,要在一块钢板上打三个孔A,B,C,已知孔心距AB=8$\sqrt{3}$mm,BC=12mm,AC=4$\sqrt{3}$mm,现孔A,B已加工完成,刀杆在B处,那么刀杆沿BA方向和垂直于BA方向各移动多少毫米才能到达C处.
如图所示,要在一块钢板上打三个孔A,B,C,已知孔心距AB=8$\sqrt{3}$mm,BC=12mm,AC=4$\sqrt{3}$mm,现孔A,B已加工完成,刀杆在B处,那么刀杆沿BA方向和垂直于BA方向各移动多少毫米才能到达C处.