题目内容
17.已知等比数列的前n项和为Sn,若S3:S2=3:2,则公比q=$1或-\frac{1}{2}$.分析 验证q=1是否满足题意,q≠1时,代入求和公式可得关于q的方程,解方程可得.
解答 解:若q=1,必有S3:S2=3a1:2a1=3:2,满足题意;
故q≠1,由等比数列的求和公式可得S3:S2=$\frac{{a}_{1}(1-{q}^{3})}{1-q}$:$\frac{{a}_{1}(1-{q}^{2})}{1-q}$=3:2,
化简可得2q2-q-1=0,解得q=-$\frac{1}{2}$,
综上,q=$1或-\frac{1}{2}$.
故答案为:$1或-\frac{1}{2}$.
点评 本题考查等比数列的前n项和公式,涉及分类讨论的思想,属中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
6.下列说法正确的是( )
| A. | log0.56>log0.54 | B. | 0.60.5>log0.60.5 | ||
| C. | 2.50<${(\frac{1}{2})^{2.5}}$ | D. | 90.9>270.48 |
15.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+\frac{1}{2}x(x<0)}\\{ln(x+1)(x≥0)}\end{array}\right.$,若函数y=f(x)-kx有3个零点,则实数k的取值范围为( )
| A. | $(0,\frac{1}{2})$ | B. | $(\frac{1}{2},1)$ | C. | (1,+∞) | D. | $(\frac{1}{4},1)$ |
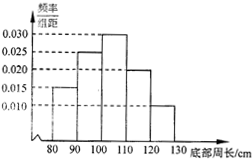 为了了解一片经济林的生长情况,随机抽 测了其中80株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的80株树木中,有32株树木的底部周长小于100cm.
为了了解一片经济林的生长情况,随机抽 测了其中80株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的80株树木中,有32株树木的底部周长小于100cm.