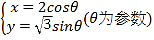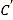题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 的切线方程;
的切线方程;
(2)讨论函数![]() 的单调性.
的单调性.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;当
上单调递减;当![]() 时,
时,![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;当
上单调递减;当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
【解析】
(1)根据导数的几何意义求解即可.
(2)易得函数定义域是![]() ,且
,且![]() .故分
.故分![]() ,
,![]() 和
和![]() 与
与![]() 四种情况,分别分析得极值点的关系进而求得原函数的单调性即可.
四种情况,分别分析得极值点的关系进而求得原函数的单调性即可.
(1)当![]() 时,
时,![]() ,则切线的斜率为
,则切线的斜率为![]() .
.
又![]() ,则曲线
,则曲线![]() 在点
在点![]() 的切线方程是
的切线方程是![]() ,
,
即![]() .
.
(2)![]() 的定义域是
的定义域是![]() .
.
![]() .
.
①当![]() 时,
时,![]() ,所以当
,所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
②当![]() 时,
时,![]() ,所以当
,所以当![]() 和
和![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
③当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上恒成立.所以
上恒成立.所以![]() 在
在![]() 上单调递增;
上单调递增;
④当![]() 时,
时,![]() ,
,
所以![]() 和
和![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
所以![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
综上所述,当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;当
上单调递减;当![]() 时,
时,![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;当
上单调递减;当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.

【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为常数且
为常数且![]() ,
,![]() 为参数).
为参数).
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 和
和![]() 相交于
相交于![]() 、
、![]() 两点,以线段
两点,以线段![]() 为一条边作
为一条边作![]() 的内接矩形
的内接矩形![]() ,当矩形
,当矩形![]() 的面积取最大值时,求
的面积取最大值时,求![]() 的值.
的值.
【题目】某手机软件研发公司为改进产品,对软件用户每天在线的时间进行调查,随机抽取40名男性与20名女性对其每天在线的时间进行了调查统计,并绘制了如图所示的条形图,其中每天的在线时间4h以上(包括4h)的用户被称为“资深用户”.
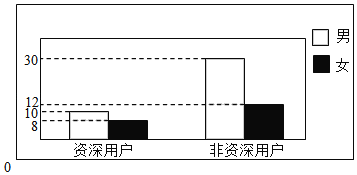
(1)根据上述样本数据,完成下面的2×2列联表,并判定是否有95%的把握认为是否为“资深用户”与性别有关;
“资深用户” | 非“资深用户” | 总计 | |
男性 | |||
女性 | |||
总计 |
(2)用样本估计总体,若从全体用户中随机抽取3人,设这3人中“资深用户”的人数为X,求随机变量X的分布列与数学期望.
附: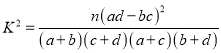 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |