题目内容
已知P是双曲线;x2-| y2 |
| 3 |
| 3 |
分析:由题意得 右焦点F(2,0),左焦点为 F′(-2,0),由双曲线的定义可得|PF′|-|PF|=2a=2,故|PF|+|PA|=|PF′|-2+|PA|≥|AF′|-2,运算求得结果.
解答:解:由题意得 右焦点F(2,0),左焦点为 F′(-2,0),
由双曲线的定义可得|PF′|-|PF|=2a=2,
|PF|+|PA|=|PF′|-2+|PA|≥|AF′|-2=
-2=2
-2,
故答案为2
-2.
由双曲线的定义可得|PF′|-|PF|=2a=2,
|PF|+|PA|=|PF′|-2+|PA|≥|AF′|-2=
| (3+2)2+3 |
| 7 |
故答案为2
| 7 |
点评:本题考查双曲线的定义和标准方程,以及双曲线的简单性质的应用,得到|PF|+|PA|=|PF′|-2+|PA|≥|AF′|-2,是解题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
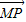 •
•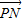 的最大值等于 .
的最大值等于 .