题目内容
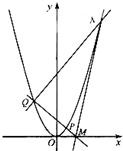
已知MN是⊙C:x2+(y-2)2=1的直径,点P是双曲线x2-y2=1上一点,则
•
的最大值等于
| MP |
| PN |
-2
-2
.分析:由题意可设直线MN所在的直线方程为x=ky-2k,联立直线与圆的方程可求M,N的坐标,然后设P(x,y),从而可表示
,
,利用向量的数量积的坐标表示可求
•
,结合二次函数的性质即可求解
| MP |
| PN |
| MP |
| PN |
解答:解:由题意可设直线MN所在的直线方程为x=ky-2k
联立
可得(y-2)2=
∴M(-k
,2-
),N(k
,2+
)
设P(x,y)则
=(x+k
,y-2+
),
=(k
-x,2+
-y)
∴则
•
=-x2+
-(2-y)2+
=-y2-1-(2-y)2+1=-2y2+4y-4
=-2(y-1)2-2≤-2
即最大值为-2
故答案为:-2
联立
|
| 1 |
| 1+k2 |
∴M(-k
|
|
|
|
设P(x,y)则
| MP |
|
|
| PN |
|
|
∴则
| MP |
| PN |
| k2 |
| 1+k2 |
| 1 |
| 1+k2 |
=-y2-1-(2-y)2+1=-2y2+4y-4
=-2(y-1)2-2≤-2
即最大值为-2
故答案为:-2
点评:本题主要考查了直线与圆相交关系的应用,向量的数量积的坐标表示的应用,还考查了一定的运算能力

练习册系列答案
相关题目
 已知抛物线C:x2=2py(p>0)上一点A(m,4)到其焦点的距离为
已知抛物线C:x2=2py(p>0)上一点A(m,4)到其焦点的距离为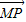 •
•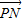 的最大值等于 .
的最大值等于 .