题目内容
设偶函数f(x)=loga|x+b|在(0,+∞)上单调递增,则f(b-2)与f(a+1)的大小关系为
| A.f(b-2)=f(a+1) | B.f(b-2)>f(a+1) |
| C.f(b-2)<f(a+1) | D.不能确 |
C
∵函数f(x)是偶函数,∴b=0,此时f(x)=loga|x|.
当a>1时,函数f(x)=loga|x|在(0,+∞)上是增函数,∴f(a+1)>f(2)=f(b-2);
当0<a<1时,函数f(x)=loga|x|在(0,+∞)上是减函数,∴f(a+1)>f(2)=f(b-2).
综上,可知f(b-2)<f(a+1).
当a>1时,函数f(x)=loga|x|在(0,+∞)上是增函数,∴f(a+1)>f(2)=f(b-2);
当0<a<1时,函数f(x)=loga|x|在(0,+∞)上是减函数,∴f(a+1)>f(2)=f(b-2).
综上,可知f(b-2)<f(a+1).

练习册系列答案
相关题目
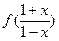 =
=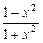 ,则
,则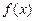 的解析式可取为
的解析式可取为 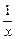 (x≤-
(x≤-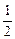 )的值域是( )
)的值域是( )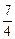
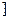
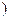
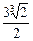 ,+∞
,+∞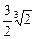 ]
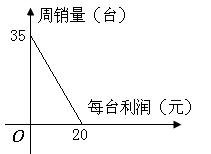
]
 与函数
与函数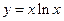 在区间
在区间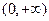 上增长较快的一个是 。
上增长较快的一个是 。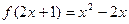 ,则
,则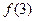 = .
= . 
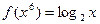 ,那么
,那么 等于( )
等于( )
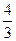 B
B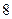 C
C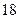 D
D