题目内容
【题目】已知数集A={a1 , a2…an}(0≤a1<a2…<an , n≥2)具有性质P;对任意的 i,j(1≤i≤j≤n),ai+aj与aj﹣ai两数中至少有一个属于A.
(1)分别判断数集{0,1,3,4}与{0,2,3,6}是否具有性质P,并说明理由;
(2)证明:a1=0,且nan=2(a1+a2+a+..+an)
(3)当n=5时若 a2=2,求集合A.
【答案】
(1)解:由于0+1,0+2,0+3,0+4,1+3,4﹣1,4﹣3,都属于数集{0,1,3,4},
∴该数集具有性质P.
由于2+3与3﹣2均不属于数集{0,2,3,6},∴该数集不具有性质P
(2)证明:令j=n,i>1,则∵“ai+aj与aj﹣ai两数中至少有一个属于A”,
∴ai+aj不属于A,∴an﹣ai属于A.
令i=n﹣1,那么an﹣an﹣1是集合A中某项,a1不行,是0,a2可以.
如果是a3或者a4,那么可知an﹣a3=an﹣1,那么an﹣a2>an﹣a3=an﹣1,只能是等于an了,矛盾.
所以令i=n﹣1可以得到an=a2+an﹣1,
同理,令i=n﹣2、n﹣3,…,2,可以得到an=ai+an+1﹣i,
∴倒序相加即可得到a1+a2+a3+…+an= ![]() an.
an.
即nan=2(a1+a2+a+..+an)
(3)解:当 n=5时,取j=5,当i≥2时,ai+a5>a5,
由A具有性质P,a5﹣ai∈A,又i=1时,a5﹣a1∈A,
∴a5﹣ai∈A,i=1,2,3,4,5
∵0=a1<a2<a3<a4<a5,∴a5﹣a1>a5﹣a2>a5﹣a3>a5﹣a4>a5﹣a5=0,
则a5﹣a1=a5,a5﹣a2=a4,a5﹣a3=a3,
从而可得a2+a4=a5,a5=2a3,故a2+a4=2a3,即0<a4﹣a3=a3﹣a2<a3,
又∵a3+a4>a2+a4=a5,∴a3+a4A,则a4﹣a3∈A,则有a4﹣a3=a2=a2﹣a1.
又∵a5﹣a4=a2=a2﹣a1,∴a5﹣a4=a4﹣a3=a3﹣a2=a2﹣a1=a2,
即a1,a2,a3,a4,a5是首项为0,公差为a2=2等差数列,
∴A={0,2,4,6,8}
【解析】(1)利用ai+aj与aj﹣ai两数中至少有一个属于A.即可判断出结论.(2)令j=n,i>1,由“ai+aj与aj﹣ai两数中至少有一个属于A”,可得an﹣ai属于A.令i=n﹣1,那么an﹣an﹣1是集合A中某项,a1不行,是0,a2可以.同理可得:令i=n﹣1可以得到an=a2+an﹣1 , 令i=n﹣2、n﹣3,…,2,可以得到an=ai+an+1﹣i , 倒序相加即可得到.(3)当 n=5时,取j=5,当i≥2时,ai+a5>a5 , 由A具有性质P,a5﹣ai∈A,又i=1时,a5﹣a1∈A,可得a5﹣ai∈A,i=1,2,3,4,5,a5﹣a1>a5﹣a2>a5﹣a3>a5﹣a4>a5﹣a5=0,则a5﹣a1=a5 , a5﹣a2=a4 , a5﹣a3=a3 , 又a3+a4>a2+a4=a5 , 可得a3+a4A,则a4﹣a3∈A,则有a4﹣a3=a2=a2﹣a1 . 可得a1 , a2 , a3 , a4 , a5是首项为0,公差为a2=2等差数列.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系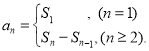 ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案