题目内容
在平面直角坐标系中,若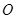 为坐标原点,则
为坐标原点,则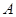 、
、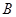 、
、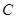 三点在同一直线上的等价条件为存在唯一的实数
三点在同一直线上的等价条件为存在唯一的实数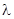 ,使得
,使得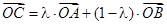 成立,此时称实数
成立,此时称实数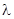 为“向量
为“向量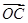 关于
关于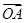 和
和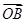 的终点共线分解系数”.若已知
的终点共线分解系数”.若已知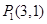 、
、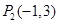 ,且向量
,且向量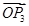 与向量
与向量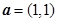 垂直,则 “向量
垂直,则 “向量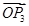 关于
关于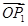 和
和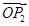 的终点共线分解系数”为( )
的终点共线分解系数”为( )
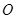 为坐标原点,则
为坐标原点,则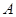 、
、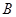 、
、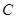 三点在同一直线上的等价条件为存在唯一的实数
三点在同一直线上的等价条件为存在唯一的实数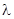 ,使得
,使得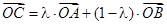 成立,此时称实数
成立,此时称实数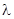 为“向量
为“向量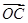 关于
关于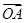 和
和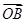 的终点共线分解系数”.若已知
的终点共线分解系数”.若已知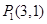 、
、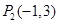 ,且向量
,且向量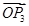 与向量
与向量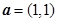 垂直,则 “向量
垂直,则 “向量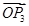 关于
关于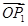 和
和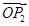 的终点共线分解系数”为( )
的终点共线分解系数”为( )A.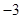 | B.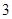 | C.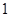 | D.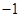 |
D
解:由向量 OP3 是直线l:x-y+10=0的法向量得出: OP3与向量 a =(1,1)垂直,
可设 OP3 =(t,-t)(t≠0),
由 OP3 =λ• OP1 +(1-λ)• OP2得(t,-t)=λ(1,3)+(1-λ)(-1,3)
=(4λ-1,3-2λ),
∴ 4λ-1="t" 3-2λ=-t ,
两式相加得2λ+2=0,
∴λ=-1.
故答案为:-1.
可设 OP3 =(t,-t)(t≠0),
由 OP3 =λ• OP1 +(1-λ)• OP2得(t,-t)=λ(1,3)+(1-λ)(-1,3)
=(4λ-1,3-2λ),
∴ 4λ-1="t" 3-2λ=-t ,
两式相加得2λ+2=0,
∴λ=-1.
故答案为:-1.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
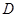 、
、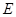 分别是
分别是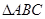 的边
的边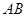 ,
,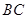 上的点,
上的点,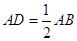 ,
,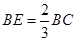 . 若
. 若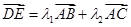 (
(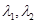 为实数),则
为实数),则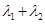 的值是
的值是 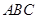 中,
中,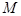 是
是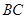 的中点,
的中点,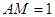 ,点
,点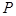 在
在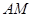 上,且满足
上,且满足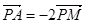 ,
,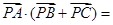 ( )
( )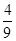
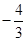
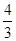
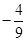
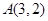 ,
,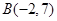 ,若直线
,若直线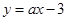 与线段
与线段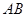 的交点
的交点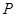 满足
满足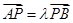 ,且
,且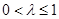 ,则实数
,则实数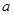 的取值范围为( )
的取值范围为( )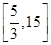
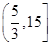
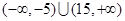
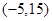
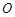 是
是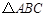 的外心,且
的外心,且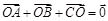 ,则
,则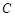 为_________.
为_________.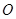 在
在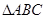 的内部,满足
的内部,满足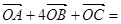 0,则
0,则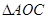 的面积之比为( )
的面积之比为( )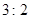
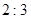
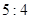
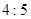
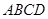 的两条对角线相交于点
的两条对角线相交于点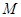 ,点
,点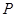 是
是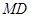 中点,若
中点,若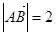 ,
,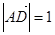 ,且
,且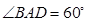 ,则
,则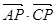 的值为
的值为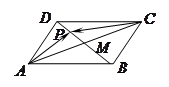




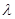 满足:
满足: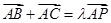 ,则
,则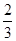
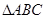 所在平面内点
所在平面内点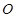 、
、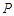 ,满足
,满足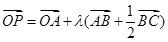 ,
, ,则点
,则点