题目内容
如图,在四棱锥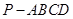 中,侧棱
中,侧棱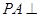 底面
底面 ,底面
,底面 为矩形,
为矩形,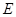 为
为 上一点,
上一点,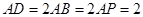 ,
,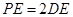 .
.
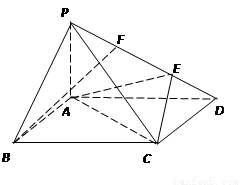
(I)若 为
为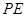 的中点,求证
的中点,求证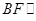 平面
平面 ;
;
(II)求三棱锥 的体积.
的体积.
【答案】
(I)详见解析;(II)三棱锥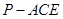 的体积为
的体积为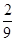 .
.
【解析】
试题分析:(I)要证线面平行,先构造面外线平行于面内线;(II)求三棱锥的体积关键是选择适当的底面,以便于求高为标准,为此要先考察线面垂直.
试题解析:(I)若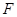 为
为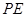 的中点,
的中点,
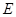 为
为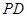 上一点,
上一点,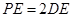 ,故
,故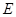 ,
,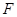 都是线段
都是线段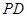 的三等分点.
的三等分点.
设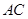 与
与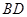 的交点为
的交点为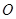 ,由于底面
,由于底面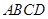 为矩形,则
为矩形,则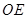 是
是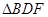 的中位线,故有
的中位线,故有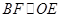 ,而
,而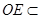 平面
平面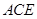 ,
,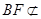 平面
平面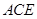 内,故
内,故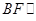 平面
平面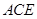 .
.
(II)由于侧棱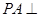 底面
底面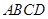 ,且
,且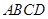 为矩形,故有
为矩形,故有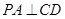 ,
,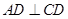 ,
,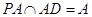 ,故
,故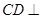 平面
平面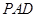 ,又因为
,又因为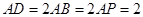 ,
,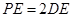 ,所以三棱锥
,所以三棱锥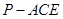 的体积
的体积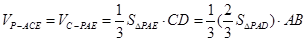
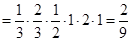 .
.
考点:直线与平面平行的判定、直线与平面垂直的判定、三棱锥的体积公式.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
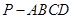 中,侧棱
中,侧棱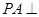 底面
底面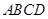 ,底面
,底面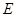 为
为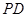 上一点,
上一点,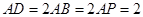 ,
,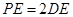 .
.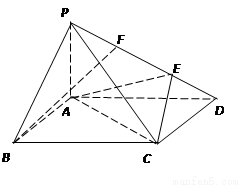
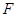 为
为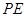 的中点,求证
的中点,求证 平面
平面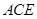 ;
; 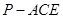 的体积.
的体积. 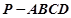 中,侧棱
中,侧棱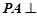 底面
底面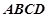 ,底面
,底面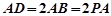 ,
,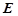 为
为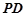 的上一点,且
的上一点,且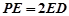 ,
,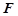 为PC的中点.
为PC的中点.

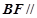 平面AEC;
平面AEC;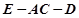 的余弦值.
的余弦值.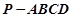 中,侧棱
中,侧棱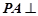 底面
底面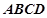 ,底面
,底面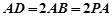 ,
,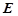 为
为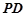 的上一点,且
的上一点,且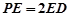 ,
,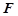 为PC的中点.
为PC的中点.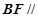 平面AEC;
平面AEC;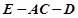 的余弦值.
的余弦值.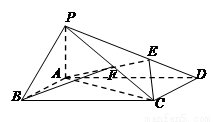
 中,侧棱
中,侧棱 底面
底面 ,底面
,底面 ,
, 为
为 的上一点,且
的上一点,且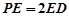 ,
, 为PC的中点.
为PC的中点. 平面AEC;
平面AEC; 的余弦值.
的余弦值.