题目内容
8本不同的书,其中有2本书是同一套书的上、下册,还有3本书是同一套书的上、中、下三册,现将它们并排放在书架的一层上,求:(1)两册一套的书排在一起的概率;
(2)三册一套的书排在一起的概率;
(3)成套的书各自排在一起的概率;
(4)两套书中至少有一套排在一起的概率;
(5)三册一套的书排在一起,而两册一套的书没有排在一起的概率.
解析:(1)将成套的两本书捆绑在一起,并设这一事件为A,则A包含的基本事件数为m=7!×2!.
∴P(A)=![]() .
.
(2)同(1),P(B)=![]() .
.
(3)P(C)=![]() .
.
(4)记两套书中至少有一套排在一起为事件D,由于“上、下两册”的书排在一起的排法数为7!×2!,“上、中、下三册”的书排在一起的排法数为6!×3!,而两套书同时各自排在一起的排法数为5!×3!×2!,同时计算了两次.
∴事件D的基本事件为
m=7!×2!+6!×3!-5!×3!×2!.
∴P(D)=![]() .
.
(5)记三册一套的书排在一起而两册一套的书没有排在一起的事件为E,将三册一套的书“捆绑”成一本书,它与其他三本单册的书的排法数为4!×3!,这四本书形成了5个空隙,将上、下册的两本书插入这5个空隙中.
∴P(E)=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
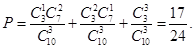 (4分)
(4分)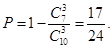 (4分)
(4分)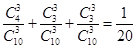 (7分
(7分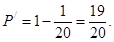 (8分)
(8分)