题目内容
1.求函数f(x)=$\frac{1+sinx+cosx}{1+sinx-cosx}$的奇偶性.分析 先根据三角函数的公式进行化简,求出函数的定义域,然后结合函数奇偶性的定义进行判断即可.
解答 解:由1+sinx-cosx=0得,
$\sqrt{2}$sin(x-$\frac{π}{4}$)=-1,
即sin(x-$\frac{π}{4}$)=-$\frac{\sqrt{2}}{2}$,
即x-$\frac{π}{4}$=$±\frac{π}{4}+kπ$,
即x=$\frac{π}{4}$$±\frac{π}{4}+kπ$,
即x=kπ+$\frac{π}{2}$或x=kπ,k∈Z,
即要使函数有意义,则x≠kπ+$\frac{π}{2}$且x≠kπ,k∈Z,
则定义域关于原点对称,
f(x)=$\frac{1+sinx+cosx}{1+sinx-cosx}$=$\frac{2sin\frac{x}{2}cos\frac{x}{2}+2co{s}^{2}\frac{x}{2}}{2sin\frac{x}{2}cos\frac{x}{2}+2si{n}^{2}\frac{x}{2}}$=$\frac{2cos\frac{x}{2}(sin\frac{x}{2}+cos\frac{x}{2})}{2sin\frac{x}{2}(sin\frac{x}{2}+cos\frac{x}{2})}$=$\frac{cos\frac{x}{2}}{sin\frac{x}{2}}$=$\frac{1}{tan\frac{x}{2}}$,
则f(-x)=$\frac{1}{tan(-\frac{x}{2})}$=-$\frac{1}{tan\frac{x}{2}}$=-f(x),
即函数f(x)是奇函数.
点评 本题主要考查函数奇偶性的判断,以及三角函数的化简,考查学生的运算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,G为MC中点,则下列结论中正确的是①②④.
如图四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,G为MC中点,则下列结论中正确的是①②④.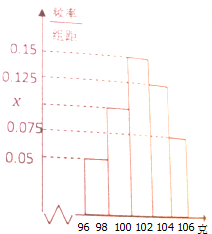 某工厂从一批产品中随机抽取40件进行检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).
某工厂从一批产品中随机抽取40件进行检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106). 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD为直角梯形,AB∥CD,∠BAD=90°,PA=AD=AB=1,CD=2,E为PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD为直角梯形,AB∥CD,∠BAD=90°,PA=AD=AB=1,CD=2,E为PC的中点.