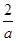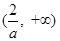题目内容
(本小题满分12分)A(理)已知函数 ,其中
,其中 .
.
(1)若存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(2)求函数 的值域.
的值域.
【答案】
(1)实数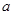 的取值范围是
的取值范围是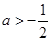 ;
;
(2) 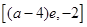
【解析】(1) 方法一:存在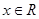 ,使得
,使得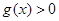 ,
,
即存在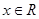 ,使得
,使得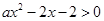 ,
,
当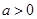 时,满足要求;
时,满足要求;
当 时,满足要求;
时,满足要求;
当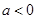 时,
时, ,解得
,解得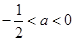
综上得,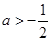 ------4分
------4分
方法二:存在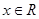 ,使得
,使得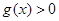 ,即存在
,即存在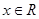 ,使得
,使得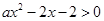
显然 ,分离参数得
,分离参数得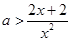 ,∴
,∴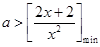
而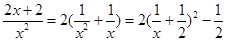 ,其中
,其中
∴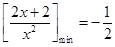
∴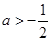 ------4分
------4分
(2) 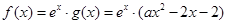
∴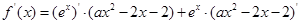 =
=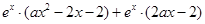
=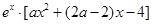 ------6分
------6分
设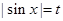 ,
, ,则转化为求函数
,则转化为求函数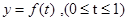 的值域.
的值域.
当 时,
时,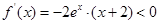 ,此时函数
,此时函数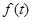 在
在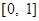 上为减函数,
上为减函数,
∴函数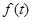 的值域为
的值域为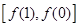 ,即
,即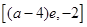
当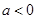 时,
时,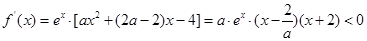
此时函数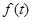 在
在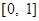 上为减函数,
上为减函数,
∴函数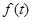 的值域为
的值域为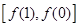 ,即
,即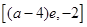 ------8分
------8分
当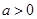 时,
时,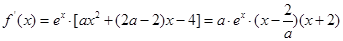
令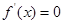 ,解得
,解得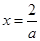 或
或 (舍).
(舍).
当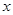 变化时,
变化时,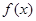 与
与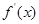 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
0 |
|
|
|
|
极小值 |
|
若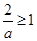 ,即
,即
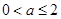 时,函数
时,函数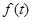 在
在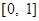 上为减函数.
上为减函数.
∴函数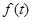 的值域为
的值域为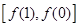 ,即
,即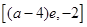
若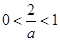 ,即
,即
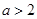 时,函数
时,函数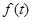 在
在 上递减,在
上递减,在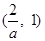 上递增
上递增
∴ 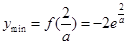
函数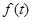 在
在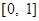 上的最大值为
上的最大值为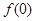 与
与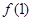 中的较大者.
中的较大者.
∵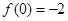 ,
,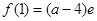 ,∴
,∴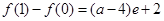
∴当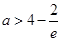 时,
时,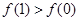 ,此时
,此时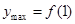
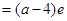 ;
;
当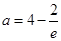 时,
时,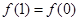 ,此时
,此时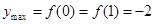 ;
;
当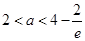 时,
时, ,此时
,此时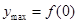
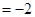 ------11分
------11分
综上,
当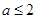 时,函数
时,函数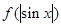 的值域为
的值域为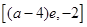 ;
;
当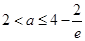 时,函数
时,函数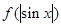 的值域为
的值域为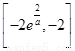 ;
;
当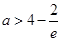 时,函数
时,函数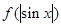 的值域为
的值域为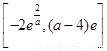 ------12分
------12分

练习册系列答案
相关题目