题目内容
若焦点在x轴的圆锥曲线
+
=1的一条准线恰好为圆x2+y2+6x-7=0的一条切线,则m的值为
或-12
或-12.
| x2 |
| 4 |
| y2 |
| m |
| 180 |
| 49 |
| 180 |
| 49 |
分析:先求圆的与坐标轴垂直的切线方程,再分类讨论圆锥曲线的准线,从而得解.
解答:解:由题意,圆的标准方程为(x+3)2+y2=16,与坐标轴垂直的切线为x=-7或x=1
当m∈(0,4)时,圆锥曲线为焦点在x轴上的椭圆,准线方程为
=-7,∴m=
;
当m∈(-∞,0)时,圆锥曲线为焦点在x轴上的双曲线,准线方程为
=1,∴m=-12
故答案为
或-12
当m∈(0,4)时,圆锥曲线为焦点在x轴上的椭圆,准线方程为
| 4 | ||
|
| 180 |
| 49 |
当m∈(-∞,0)时,圆锥曲线为焦点在x轴上的双曲线,准线方程为
| 4 | ||
|
故答案为
| 180 |
| 49 |
点评:本题以圆锥曲线为载体,考查圆与圆锥曲线的综合,关键是分类讨论,求准线方程.

练习册系列答案
相关题目
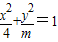 的一条准线恰好为圆x2+y2+6x-7=0的一条切线,则m的值为 .
的一条准线恰好为圆x2+y2+6x-7=0的一条切线,则m的值为 .