Question

【题目】过P（2，1）且两两互相垂直的直线l1 ， l2分别交椭圆 + =1于A，B与C，D．
（1）求|PA||PB|的最值；
（2）求证： + 为定值．

Answer 1

【答案】
（1）解：设直线l1的倾斜角为θ，则l1的参数方程为 （t为参数）

代入椭圆的方程 中，整理得：（cos2θ+4sin2θ）t2+（4cosθ+8sinθ）t﹣8=0，

∴由韦达定理可知：tAtB=﹣ ，

∴|PA||PB|= = ，

故|PA||PB|的最大值为8，最小值为2

（2）解：∵l1⊥l2，不妨设l1的倾斜角小于l2的倾斜角，

则l2的倾斜角为 +θ，

因此直线l2的参数方程为 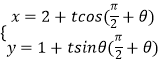（t为参数）

代入椭圆的方程 + =1，

整理得：（sin2θ+4cos2θ）t2+4（2cosθ﹣sinθ）t﹣8=0，

∴|PC||PD|=丨tCtD丨= ，

∴ + = + = ，

∴ + 为定值

【解析】（1）由题意设出直线l1的参数方程，代入椭圆方程，利用韦达定理求得tAtB=﹣ ，由|PA||PB|= = ，根据正弦函数图象及性质即可求得|PA||PB|的最值；（2）由l1⊥l2 ， 求得l2的参数方程，并根据韦达定理求得|PC||PD|=丨tCtD丨= ，表示出 + ，根据同角三角函数基本关系即可求证 + 为定值．