题目内容

若△ABC的三个内角满足SinA：sinB：SinC=6：12：15，则△ABC（　　）
A．一定是锐角三角形
B．一定是直角三角形
C．一定是钝角三角形
D．可能是锐角三角形也可能是钝角三角形
∵角A、B、C满足SinA：sinB：SinC=6：12：15，
∴根据正弦定理，得a：b：c=6：12：15，
设a=6x，b=12x，c=15x，由余弦定理得：cosC=
a2+b2-c2
2ab
=
36x2+144x2-255x2
2•6x•12x
=-
25
48
，
∵C是三角形内角，得C∈（0，π），
∴由cosC=-
25
48
＜0，得C为钝角
因此，△ABC是钝角三角形
故选：C．
练习册系列答案
相关题目
阅读与理解：asinx+bcosx=
a2+b2
sin(x+φ)给出公式：
我们可以根据公式将函数g(x)=sinx+
3
cosx化为：g(x)=2(
1
2
sinx+
3
2
cosx)=2(sinxcos
π
3
+cosxsin
π
3
)=2sin(x+
π
3
)
（1）根据你的理解将函数f(x)=
3
2
sinx+
3
2
cosx化为f（x）=Asin（ωx+φ）的形式．
（2）求出上面函数f（x）的最小正周期、对称中心及单调递增区间．
已知cosα=-
4
5
，α为第三象限角，则tanα=（　　）
A．
3
4
B．-
3
4
C．
4
3
D．-
4
3
若三条线段的长分别为7、8、9，则用这三条线段（　　）
A．能组成直角三角形B．能组成锐角三角形
C．能组成钝角三角形D．不能组成三角形
△ABC中，已知（a+b）：（b+c）：（c+a）=6：4：5，给出下列结论：
①这个三角形被唯一确定
②△ABC是钝角三角形
③sinA：sinB：sinC=7：5：3
其中正确结论的序号是______．
（1）已知tanα=
1
3
，求
1
2sinαcosα+cos2α
的值；
（2）化简：
tan(π-α)cos(2π-α)sin(-α+
3
2
π)
cos(-α-π)sin(-π-α)
．
已知：函数f(x)=2
3
sin2x+
cos3x
cosx
．
（1）求函数f（x）的最大值及此时x的值；
（2）在△ABC中，a，b，c分别为内角A，B，C所对的边，且对f（x）定义域中的任意的x都有f（x）≤f（A）．现在给出三个条件：①a=2；②B=45°；③c=
3
b，试从中选出两个可以确定△ABC的条件，写出你的选择并以此为依据求△ABC的面积．（只需写出一个选定方案即可）
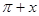不等式sin()>0成立的x的取值范围为(   )
A．B．
C．D．
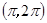
已知，则（ ）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网