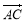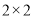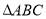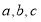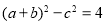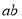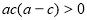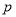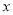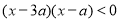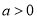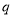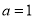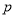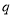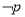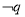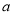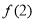题目内容
已知点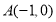 、
、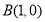 ,动点
,动点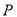 满足:
满足: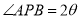 ,且
,且
(1)求动点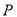 的轨迹
的轨迹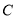 的方程;
的方程;
(2)已知圆W: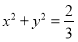 的切线
的切线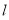 与轨迹
与轨迹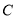 相交于P,Q两点,求证:以PQ为直径的圆经过坐标原点
相交于P,Q两点,求证:以PQ为直径的圆经过坐标原点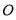 .
.
(1) ;(2)证明详见解析.
;(2)证明详见解析.
【解析】
试题分析:(1)针对 点的位置:点
点的位置:点 在线段
在线段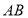 上、点
上、点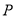 在
在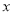 轴上且在线段
轴上且在线段 外、点
外、点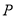 不在
不在 轴上进行分类确定
轴上进行分类确定 点的轨迹,前两种只须简单的检验即可,当点
点的轨迹,前两种只须简单的检验即可,当点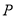 不在
不在 轴上时,在
轴上时,在 中,应用余弦定理得
中,应用余弦定理得 ,化简得到
,化简得到 ,再根据圆锥曲线的定义,可知动点
,再根据圆锥曲线的定义,可知动点 在以
在以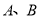 为两焦点的椭圆上,由椭圆的相关参数即可写出椭圆的方程,最后综合各种情况写出所求轨迹的方程;(2)先验证直线
为两焦点的椭圆上,由椭圆的相关参数即可写出椭圆的方程,最后综合各种情况写出所求轨迹的方程;(2)先验证直线 斜率不存在与斜率为0的情形,然后再证明直线
斜率不存在与斜率为0的情形,然后再证明直线 斜率存在且不为0的情况,此时先设直线
斜率存在且不为0的情况,此时先设直线 ,设点
,设点 ,联立直线与轨迹
,联立直线与轨迹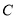 的方程,消去
的方程,消去 得到
得到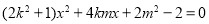 ,进而求出
,进而求出 及
及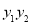 ,得到
,得到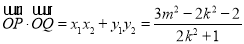 ,利用直线与圆相切得到
,利用直线与圆相切得到 ,代入
,代入 式子中,即可得到
式子中,即可得到 ,从而问题得证.
,从而问题得证.
试题解析:(1)①当点 在线段
在线段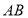 上时
上时
 不存在或
不存在或 ,均不满足题目条件 1分
,均不满足题目条件 1分
②当点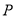 在
在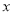 轴上且在线段
轴上且在线段 外时,
外时,
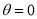 ,设
,设
由 可得
可得 ∴
∴ ∴
∴ 3分
3分
③当点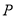 不在
不在 轴上时,
轴上时,
在 中,由余弦定理得
中,由余弦定理得


 ,即动点
,即动点 在以
在以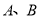 为两焦点的椭圆上
为两焦点的椭圆上
方程为: (
(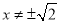 )
)
综和①②③可知:动点 的轨迹
的轨迹 的方程为:
的方程为: 6分
6分
(2)①当直线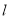 的斜率不存在时
的斜率不存在时
∵直线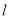 与圆
与圆 相切,故切线方程为
相切,故切线方程为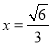 或
或
切线方程与 联立方程组
联立方程组
可求得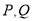 为
为 或
或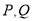 为
为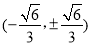
则以 为直径的圆的方程为
为直径的圆的方程为 ,经过坐标原点
,经过坐标原点
②当直线 的斜率为零时
的斜率为零时
与①类似,
可求得以 为直径的圆的方程为
为直径的圆的方程为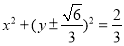 ,经过坐标原点
,经过坐标原点 10分
10分
③当直线 的斜率存在且不为零时设直线
的斜率存在且不为零时设直线 的方程为
的方程为
由 消去
消去 得
得
设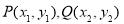 ,则
,则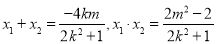
∴
∴ ①
①
∵直线 和圆
和圆 相切
相切
∴圆心到直线 的距离
的距离 ,整理得
,整理得 ②
②
将②式代入①式,得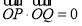 ,显然以
,显然以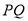 为直径的圆经过坐标原点
为直径的圆经过坐标原点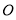
综上可知,以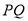 为直径的圆经过坐标原点
为直径的圆经过坐标原点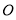 14分.
14分.
考点:1.轨迹的求法;2.椭圆的标准方程;3.直线与圆的位置关系;4.直线与圆锥曲线的综合问题.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案