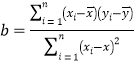题目内容
【题目】已知椭圆
与双曲线
有公共的焦点，
的一条渐近线与以
的长轴为直径的圆相交于
两点，若恰好将线段
三等分，则
A.
B.
C.
D.
【答案】B
【解析】
先由双曲线方程确定一条渐近线方程为y=2x，根据对称性易知AB为圆的直径且AB=2a，利用椭圆与双曲线有公共的焦点，得方程a2-b2=5；设C1与y=2x在第一象限的交点的坐标，代入C1的方程得；由对称性求得直线y=2x被C1截得的弦长，根据C1恰好将线段AB三等分得出a2，b2的值，故可得结论．
由题意, C2的焦点为
，一条渐近线方程为y=2x，根据对称性易知AB为圆的直径且AB=2a
∴C1的半焦距
,于是得
①
设C1与y=2x在第一象限的交点的坐标为(m,2m),代入C1的方程得：
②，
由对称性知直线y=2x被C1截得的弦长
，
由题得：
,所以
③
由②③得
④
由①④得
故选C
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某公司计划购买1台机器，该种机器使用三年后即被淘汰.在购进机器时，可以一次性额外购买
次维修，每次维修费用300元，另外实际维修一次还需向维修人员支付上门服务费80元.在机器使用期间，如果维修次数超过购买的次时，则超出的维修次数，每次只需支付维修费用700元，无需支付上门服务费.需决策在购买机器时应同时一次性购买几次维修，为此搜集并整理了100台这种机器在三年使用期内的维修次数，得到下面统计表：
维修次数 | 6 | 7 | 8 | 9 | 10 |
频数 | 10 | 20 | 30 | 30 | 10 |
记
表示1台机器在三年使用期内的维修次数，
表示1台机器维修所需的总费用（单位：元）.
（1）若
，求与的函数解析式；
（2）假设这100台机器在购机的同时每台都购买8次维修，或每台都购买9次维修，分别计算这100台机器在维修上所需总费用的平均数，并以此作为决策依据，购买1台机器的同时应购买8次还是9次维修？
