题目内容
如图所示,在直角梯形ABCD中,∠BAD=∠ADC=90°,CD=DA=a,AB=2a,SA⊥平面ABCD,且SA=a,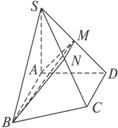
(1)求证:△SAD、△SAB、△SDC、△SCB都是直角三角形;
(2)在SD上取点M,SC交平面ABM于N,求证:四边形ABNM是直角梯形;
(3)若SM=x,写出BM=f(x)的表达式,并求当x为何值时,BM最小?最小值是多少?
(1)证明:∵SA⊥平面ABCD,∴SA⊥AD,SA⊥AB.
∴△SAD、△SAB是直角三角形.
又CD⊥AD,
∴CD⊥SD(三垂线定理).
故△SDC是直角三角形.
在Rt△SAD中, ![]() ;
;
在Rt△SDC中,![]() ;
;
在Rt△SAB中,![]() .
.
在直角梯形ABCD中,
![]() .
.
∴SC2+BC2=SB2,故△SCB是直角三角形.
(2)证明:∵CD∥AB,∴CD∥平面ABNM.
又CD![]() 平面SCD,且平面SCD∩平面ABNM=MN,
平面SCD,且平面SCD∩平面ABNM=MN,
∴CD∥MN.∴AB∥MN.
又MN<CD<AB,
∴四边形ABNM为梯形.
∵AB⊥SA,AB⊥AD,
∴AB⊥平面SAD.∴AB⊥AM.
故四边形ABNM为直角梯形.
(3)解:在△SAM中,∠ASM=45°,SA=a,SM=x,
由余弦定理得AM2=x2+a2-2axcos45°=x2+a2-![]() .
.
在Rt△BAM中,![]() ,
,
∴当x=![]() 时,BMmin=
时,BMmin=![]() ,
,
即当x为![]() 时,BM最小,最小值为
时,BM最小,最小值为![]() .
.

练习册系列答案
相关题目
 如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=
如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=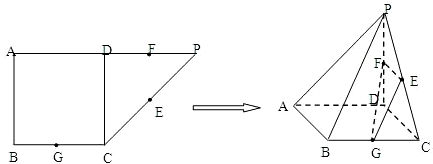
 如图所示,在直角梯形OABC中,
如图所示,在直角梯形OABC中,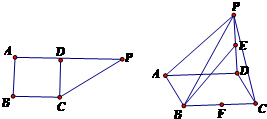 如图所示,在直角梯形ABCP中,AP∥BC,AB⊥AP,AB=BC=3,AP=7,CD⊥AP,现将△PCD沿折线CD折成直二面角P-CD-A,设E,F分别是PD,BC的中点.
如图所示,在直角梯形ABCP中,AP∥BC,AB⊥AP,AB=BC=3,AP=7,CD⊥AP,现将△PCD沿折线CD折成直二面角P-CD-A,设E,F分别是PD,BC的中点.